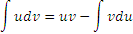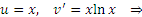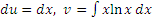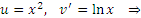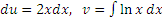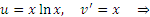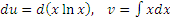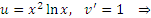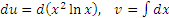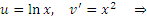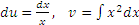|
Формула интегрирования по частям есть не что иное как правило дифференцирования произведения двух функций, выраженное в интегральной форме:
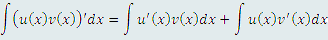 , ,
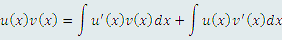
|
|||||
Формула интегрирования по частям имеет вид
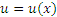 и и 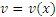 - произвольные дифференцируемые функции. - произвольные дифференцируемые функции.
Формула (1) позволяет свести одну проблему интегрирования к другой. Вывод этой формулы достаточно прост: 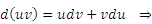
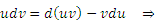
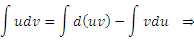
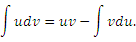
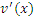 : :
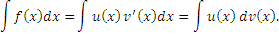
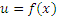 , что означает , что означает 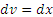 , , 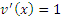 . .
Во-вторых, чтобы найти 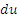 и и 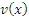 , нужно продифференцировать u(x) и проинтегрировать , нужно продифференцировать u(x) и проинтегрировать 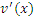 : :
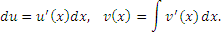
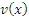 постоянную интегрирования можно положить равной нулю.) постоянную интегрирования можно положить равной нулю.)
Самым сложным этапом метода интегрирования по частям является выбор функций u(x) и 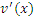 , поскольку не существует универсального правила, применимого во всех случаях. Понимание приходит только с опытом. Поэтому на первой стадии ознакомления с методом нужно какой-нибудь выбор и посмотреть – будет ли полученный интеграл проще исходного. Если нет, то сделайте другой выбор, перебирая различные варианты до тех пор, пока не будет найден наилучший. Обычно достаточно решить несколько примеров, чтобы научиться сразу делать правильный выбор. В качестве ориентиров можно использовать следующие простые критерии. , поскольку не существует универсального правила, применимого во всех случаях. Понимание приходит только с опытом. Поэтому на первой стадии ознакомления с методом нужно какой-нибудь выбор и посмотреть – будет ли полученный интеграл проще исходного. Если нет, то сделайте другой выбор, перебирая различные варианты до тех пор, пока не будет найден наилучший. Обычно достаточно решить несколько примеров, чтобы научиться сразу делать правильный выбор. В качестве ориентиров можно использовать следующие простые критерии.
(A): Интеграл от 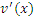 должен вычисляться достаточно просто. должен вычисляться достаточно просто.
(B): Производная от u(x) должна быть достаточно простой функцией - желательно, более простой, чем сама функция u(x). В качестве примера применения метода интегрирования по частям обсудим подробно процедуру вычисление интеграла 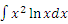 . .
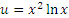 в виде произведения в виде произведения 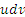 : :
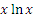 и от и от 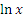 слишком сложны. слишком сложны.
Варианты (3) и (4) противоречат критерию (B) и только пятый вариант приемлем во всех отношениях. Действительно, во-первых, степенная функция 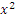 легко интегрируется: легко интегрируется:
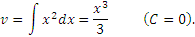
Во-вторых, производной от ln x является рациональная функция 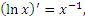 которая, безусловно, значительно проще логарифмической функции. которая, безусловно, значительно проще логарифмической функции.
Применяя формулу интегрирования по частям, получаем 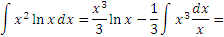
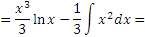
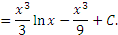
|