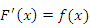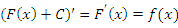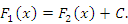|
Рассмотрим уравнение
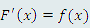 , ,
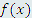 рассматривается в качестве заданной, а искомая функция рассматривается в качестве заданной, а искомая функция 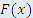 входит под знак производной. входит под знак производной.
Решение этого уравнения и представляет собой задачу о нахождении первообразной 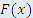 для заданной функции для заданной функции 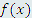 . .
|
|||||||||||||
Пусть функция 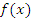 определена на некотором промежутке D. Функция определена на некотором промежутке D. Функция 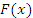 называется первообразной функции называется первообразной функции 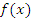 , если , если
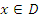 . .
Если к первообразной 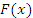 функции функции 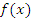 прибавить любую постоянную C, то полученная функция прибавить любую постоянную C, то полученная функция 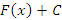 также является первообразной, поскольку также является первообразной, поскольку
Любые две первообразные одной и той же функции отличаются друг от друга не более чем на постоянную величину C. Действительно, пусть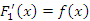 и и 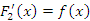 для всех для всех 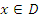 . .
Тогда 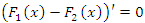 и, следовательно, разность и, следовательно, разность 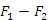 есть величина постоянная: есть величина постоянная:
|