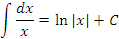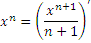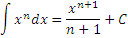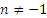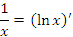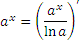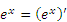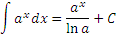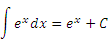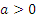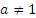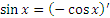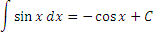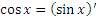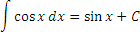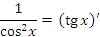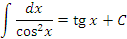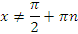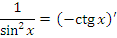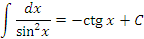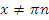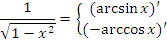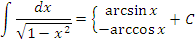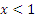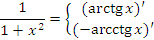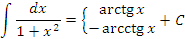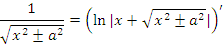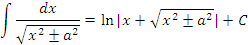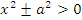|
Равенства
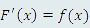
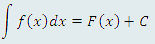
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Возьмем за основу таблицу основных производных и представим каждую формулу вида 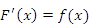 равносильным интегральным равенством равносильным интегральным равенством 
Справедливость представленных в таблице интегралных формул легко проверяется непосредственным дифференцированием. В частности, 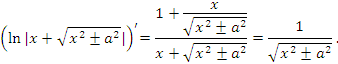
|
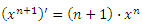
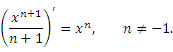
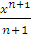 является первообразной для
является первообразной для 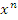 и, следовательно,
и, следовательно,
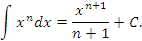
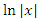 вляется первообразной для функции
вляется первообразной для функции 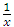 при любых
при любых 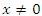 .
.
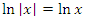 и
и 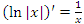 .
.
 и
и 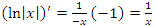 .
.