|
Следует иметь в виду, что во многих случаях для интегрирования функции достаточно предварительно выполнить некоторые элементарные преобразования, основанные на алгебраических или тригонометрических тождествах.
Примеры таких преобразований: |
|
|
Чтобы продифференцировать какую-либо функцию, достаточно следовать простым правилам. При этом вид дифференцируемой функции практически несущественен – с точки зрения самой возможности получения результата.
Совсем не так обстоит дело с интегрированием функций. Например, легко продифференцировать функцию 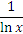 , однако интеграл от этой функции является неберущимся – в том смысле, что его нельзя представить в виде конечной комбинации элементарных функций. , однако интеграл от этой функции является неберущимся – в том смысле, что его нельзя представить в виде конечной комбинации элементарных функций.
Не существует универсального рецепта, пригодного для интегрирования любой функции. В каких-то случаях достаточно выполнить простые преобразования подынтегрального выражения или же разложить интегрируемую дробь на сумму простых дробей. Например, для интегрирования функции К наиболее важным методам интегрирования относятся
|
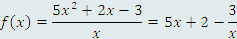
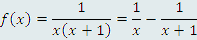
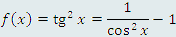
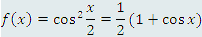
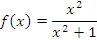 достаточно представить ее в виде
достаточно представить ее в виде 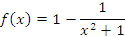 и воспользоваться свойством интеграла от разности функций.
и воспользоваться свойством интеграла от разности функций.