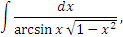|
Пусть функция F(x) является первообразной функции f(x). Это означает, что
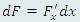 . Однако первый дифференциал функции сохраняет свою форму вне зависимости от того, является ли x независимой переменной или же функцией некоторой переменной. Поэтому равенство . Однако первый дифференциал функции сохраняет свою форму вне зависимости от того, является ли x независимой переменной или же функцией некоторой переменной. Поэтому равенство
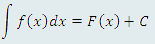
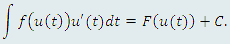

 преобразуется к табличному виду преобразуется к табличному виду

 получаем получаем
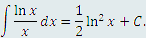
|
|||||||||||||||||
|
Если произвольным образом задать функцию, то в подавляющем большинстве случаев интеграл от такой функции будет неберущимся - в том смысле, что не существует какой-либо конечной комбинации элементарных функций, производная от которой равнялась бы этой функции.
Некоторым таким неберущимся интегралам присваивают персональные имена и называют их специальными функциями. Из соображений удобства подстановки можно подразделить на два типа: 1) 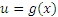 ; 2) ; 2) 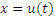 . .
В обоих случаях речь идет о замене переменной, а различие заключается только в технике реализации этой замены.
 , которая влечет , которая влечет 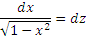 и, следовательно, и, следовательно,
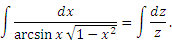
Подстановка была вынужденной, но оказалась удачной: интеграл приведен к табличному виду. Все оказалось внутренне согласованным – нужный радикал в нужном месте в комбинации с нужной функцией. Достаточно, например, заменить единицу под знаком корня на любое другое число или же изменить степень корня, чтобы превратить интеграл в не берущийся. Так, любой из нижеприведенных интегралов является неберущимся: 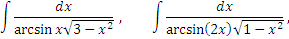
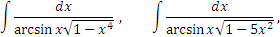

Обсудим другой прием, позволяющий непосредственным образом выйти на разумную подстановку. Обратимся вновь к интегралу (4) и представим подынтегральное выражение в виде 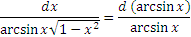
Теперь переменная x входит только под знак арксинуса и последующие действмя представляются вполне очевидными. В таких случаях говорят, что мы "подвели множитель 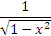 под знак дифференциала". под знак дифференциала".
Другие примеры: 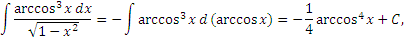

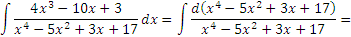
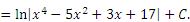
|
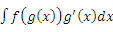 .
.
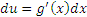 , получаем более простой интеграл
, получаем более простой интеграл
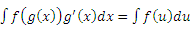

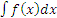 к другому виду:
к другому виду:
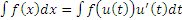 .
.