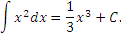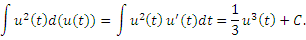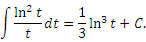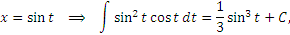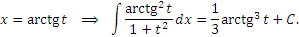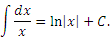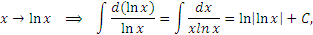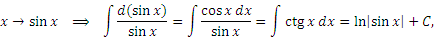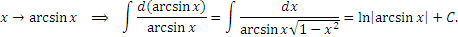|
Как правило, один и тот же интеграл можно вычислить с помощью различного рода подстановок. Например, интеграл
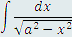 приводится к табличному виду подстановкой x = at : приводится к табличному виду подстановкой x = at :
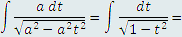
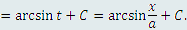
 , то рассматриваемый интеграл преобразуется к предельно простому виду: , то рассматриваемый интеграл преобразуется к предельно простому виду:
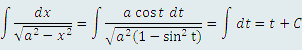 . .
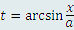 получаем получаем
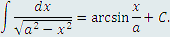
|
|||||||||||||||||||||||||||||||||||||
Рассмотрим табличный интеграл
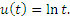 Тогда Тогда
Аналогично,
Взяв за основу простые интегралы (с известными ответами) и преобразовав их в “сложные”, мы окольным путем вычислили эти “сложные” интегралы. Можно интерпретировать наши действия и как составление задач на интегрирование – тем более, что в реальности это примерно так и происходит. Нам осталось только воспользоваться какой-нибудь фразой типа “Вычислить методом замены переменной следующие интегралы”. Сами же интегралы у нас уже имеются: 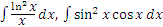 и т.д. и т.д.
Такой подход к составлению задач обладает целым рядом преимуществ:
|