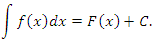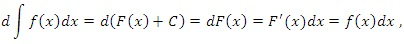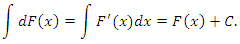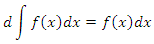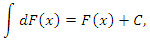|
Если функция
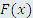 является первообразной функции является первообразной функции 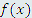 , то и любая другая функция, отличающаяся от , то и любая другая функция, отличающаяся от 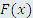 на постоянное слагаемое, является первообразной функции на постоянное слагаемое, является первообразной функции 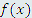 . .
Выражение 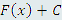 описывает всю совокупность первообразных функции описывает всю совокупность первообразных функции 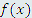 и называется непределенным интегралом от функции и называется непределенным интегралом от функции 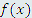 . .
|
|||||||||||||||||||||
Совокупность всех первообразных функции 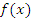 называется неопределенным интегралом от называется неопределенным интегралом от 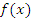 и обозначается символическим выражением и обозначается символическим выражением 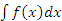 , которое читается "интеграл от эф от икс по дэ икс". , которое читается "интеграл от эф от икс по дэ икс".
Если 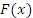 – одна из первообразных некоторой функции – одна из первообразных некоторой функции 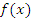 , то совокупность всех первообразных этой функции можно представить в виде , то совокупность всех первообразных этой функции можно представить в виде 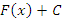 , где C – произвольная постоянная. , где C – произвольная постоянная.
Таким образом,
Приведем некоторые терминологические выражения: 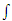 – знак интеграла; – знак интеграла;
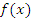 – подынтегральная функция; – подынтегральная функция;
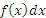 – подынтегральное выражение; – подынтегральное выражение;
x – переменная интегрирования; C – постоянная интегрирования; Легко убедиться в том, что дифференцирование и интегрирование представляют собой взаимно обратные операции. Действительно,
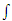 как бы взаимно сокращаются. При этом операция дифференцирования возвращает выражение, предшествующее его интегрированию, тогда как операция интегрирования возвращает предшествующее дифференцированию выражение с точностью до постоянного слагаемого, что находится в полном соответствии с определением (1). как бы взаимно сокращаются. При этом операция дифференцирования возвращает выражение, предшествующее его интегрированию, тогда как операция интегрирования возвращает предшествующее дифференцированию выражение с точностью до постоянного слагаемого, что находится в полном соответствии с определением (1).
|