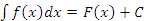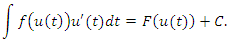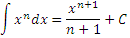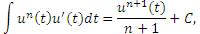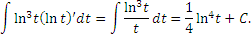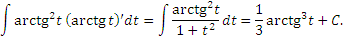|
Напоиним, что первый дифференциал функции F(x) сохраняет свою форму вне зависимости от того, является ли x независимой переменной или же функцией некоторой переменной:
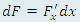
|
|||||||||||||||||||||||||
Согласно обному из свойств неопределенных интегралов, равенство
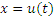 : :
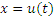 . Такой подход позволяет расширить таблицу интегралов и оказывается конструктивным при составлении задач. . Такой подход позволяет расширить таблицу интегралов и оказывается конструктивным при составлении задач.
Разъясним эти соображения на примере интеграла от степенной функции,
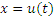 , получаем новую формулу, , получаем новую формулу,
В качестве функции 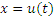 может выступать любая функция, имеющая на соответствующем промежутке непрерывную производную. может выступать любая функция, имеющая на соответствующем промежутке непрерывную производную.
Пусть, в частности, n = 3 и 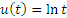 . Тогда . Тогда
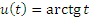 имеем имеем
|