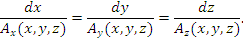Векторное поле может иметь весьма сложный характер, изменяясь по величине и направлению при переходе от от одной точки к другой.
 Для наглядного представления векторного поля мохно начертить в различных точках пространства векторы, показывающие направления поля в этих точках.
Для наглядного представления векторного поля мохно начертить в различных точках пространства векторы, показывающие направления поля в этих точках.

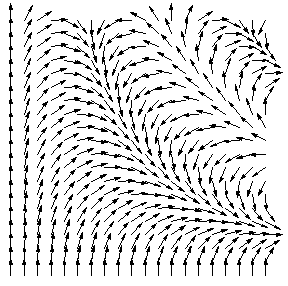
 Рис. 1
Рис. 1. Наглядная картина векторного поля.
(Для просмотра другого варианта векторного поля подведите курсор к рисунку.)
 Можно также использовать векторные линии, представляющие собой кривые, касательные к которым в любой точке совпадают с напрвлением поля в этой точке. Эти линии как бы следуют за стрелками, выдерживая направление поля.
Можно также использовать векторные линии, представляющие собой кривые, касательные к которым в любой точке совпадают с напрвлением поля в этой точке. Эти линии как бы следуют за стрелками, выдерживая направление поля.

|
|
|
|
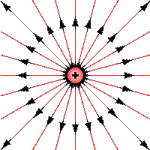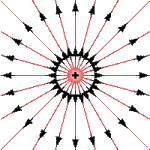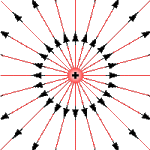
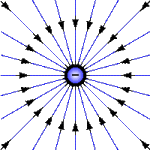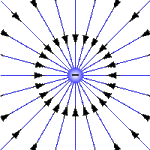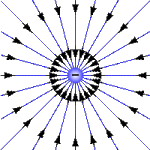
Рис. 2. Векторные (силовые) линии поля изолированного положительного заряда имеют вид лучей, исходящих из точки расположения заряда.
 (Для получения "стоп-кадра" поместите курсор в область расположения рисунка.)
(Для получения "стоп-кадра" поместите курсор в область расположения рисунка.)
|
|
Рис. 3. Векторные (силовые) линии поля изолированного отрицательного заряда изображается в виде пучка лучей, сходящихся в точке расположения заряда.
 (Для получения "стоп-кадра" поместите курсор в область расположения рисунка.)
(Для получения "стоп-кадра" поместите курсор в область расположения рисунка.)
|
 Электрическое поле в любой точке пространства равно векторной сумме полей, созданных каждым зарядом в отдельности. Касательная, проведенная к силовой линии в любой ее точке, показывает направление действия силы со стороны злектрического поля на положительно заряженную частицу, помещенную в данную точку.
Электрическое поле в любой точке пространства равно векторной сумме полей, созданных каждым зарядом в отдельности. Касательная, проведенная к силовой линии в любой ее точке, показывает направление действия силы со стороны злектрического поля на положительно заряженную частицу, помещенную в данную точку.

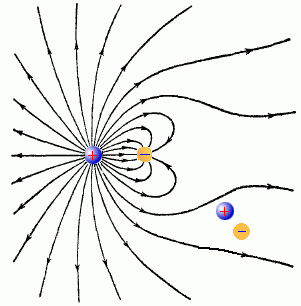
 Рис. 4
Рис. 4. Векторные линии электрического поля системы четырех заряженных частиц.
(Для просмотра векторной картины поля системы двух заряженных частиц подведите курсор к рисунку.)
 Заметим, что через одну точку может проходить только одна векторная линия. В противном случае в точке пересечения векторных линий вектор поля A имел бы одновременно различные направления. Исключения составляют точечные источники поля, примерами которых могут служить электрические заряды. Источники поля являются точками сгущения векторных линий: в них эти линии начинаются или заканчиваются. В тех местах, где поле мало, векторные линии проводятся реже, а там, где поле велико – гуще.
Заметим, что через одну точку может проходить только одна векторная линия. В противном случае в точке пересечения векторных линий вектор поля A имел бы одновременно различные направления. Исключения составляют точечные источники поля, примерами которых могут служить электрические заряды. Источники поля являются точками сгущения векторных линий: в них эти линии начинаются или заканчиваются. В тех местах, где поле мало, векторные линии проводятся реже, а там, где поле велико – гуще.
 Очевидно, что вектор
Очевидно, что вектор 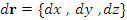 , проведенный из некоторой точки P (x, y, z) векторной линии поля A в бесконечно близко расположенную точку этой линии, является касательным вектором и, следовательно, параллелен вектору A (P), что означает пропорциональность соответствующих координат двух векторов:
Эти равенства называются уравнениями векторных линий поля A и представляют собой систему двух дифференциальных уравнений. , проведенный из некоторой точки P (x, y, z) векторной линии поля A в бесконечно близко расположенную точку этой линии, является касательным вектором и, следовательно, параллелен вектору A (P), что означает пропорциональность соответствующих координат двух векторов:
Эти равенства называются уравнениями векторных линий поля A и представляют собой систему двух дифференциальных уравнений.
 Если выбрать некоторую замкнутую кривую, отличную от векторной линии, и провести через каждую ее точку векторную линию, то получится трубчатая поверхность, называемая векторной трубкой.
Если выбрать некоторую замкнутую кривую, отличную от векторной линии, и провести через каждую ее точку векторную линию, то получится трубчатая поверхность, называемая векторной трубкой.

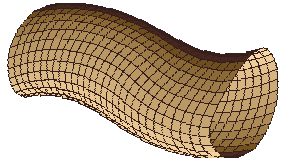
 Рис. 5
Рис. 5. Векторная трубка.
Свойства векторных трубок поля обсуждаются в разделе "Соленоидальное поле".
|


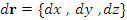 , проведенный из некоторой точки P (x, y, z) векторной линии поля A в бесконечно близко расположенную точку этой линии, является касательным вектором и, следовательно, параллелен вектору A (P), что означает пропорциональность соответствующих координат двух векторов:
, проведенный из некоторой точки P (x, y, z) векторной линии поля A в бесконечно близко расположенную точку этой линии, является касательным вектором и, следовательно, параллелен вектору A (P), что означает пропорциональность соответствующих координат двух векторов: