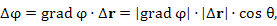Рассмотрим изменение скалярного поля 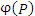 при смещении из точки при смещении из точки 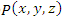 на малый вектор на малый вектор 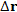 в близко расположенную точку в близко расположенную точку 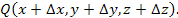

 Используя формулу Тейлора
Используя формулу Тейлора
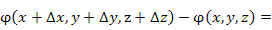
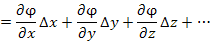 ,
изменение функции 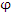 можно представить в виде
Выражение в правой части этого равенства можно интерпретировать как скалярное произведение векторов, одним из которых является вектор смещения можно представить в виде
Выражение в правой части этого равенства можно интерпретировать как скалярное произведение векторов, одним из которых является вектор смещения 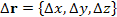 , а другим – вектор , а другим – вектор 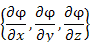 , называемый градиентом скалярного поля:
Таким образом, , называемый градиентом скалярного поля:
Таким образом,
| |
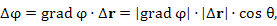
|
(1) |
|
где θ – угол между векторами 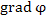 и и 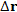 . .
 Из равенства (1) следует, что изменение
Из равенства (1) следует, что изменение 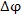 принимает наибольшее значение, если направление вектора смещения принимает наибольшее значение, если направление вектора смещения 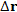 совпадает с направлением совпадает с направлением 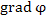 . Другими словами, вектор grad φ направлен в сторону наиболее быстрого возрастания функции φ, а его величина . Другими словами, вектор grad φ направлен в сторону наиболее быстрого возрастания функции φ, а его величина 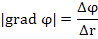 равна быстроте изменения функции равна быстроте изменения функции 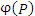 в этом направлении. в этом направлении.
 Для большей наглядности предположим, что скалярное поле
Для большей наглядности предположим, что скалярное поле 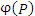 задано в плоской области. Тогда уравнение задано в плоской области. Тогда уравнение 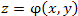 описывает некоторую поверхность в трехмерном пространстве. описывает некоторую поверхность в трехмерном пространстве.
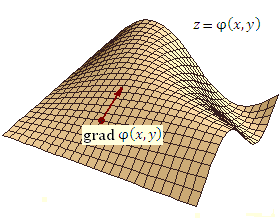 Рис. 1
Рис. 1. Направление вектора 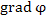 в некоторой точке показано стрелкой.
 Если вообразить себя находящимся в какой-то точке этой поверхности, то легко понять, что только в одном из направлений за один шаг можно подняться выше, чем за такой же шаг в любом другом направлении. Направление с наивысшей крутизной и является направлением вектора
Если вообразить себя находящимся в какой-то точке этой поверхности, то легко понять, что только в одном из направлений за один шаг можно подняться выше, чем за такой же шаг в любом другом направлении. Направление с наивысшей крутизной и является направлением вектора 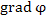 , а величина градиента определяется тангенсом угла наклона, соответствующего этому направлению. , а величина градиента определяется тангенсом угла наклона, соответствующего этому направлению.
|
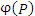 при смещении из точки
при смещении из точки 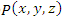 на малый вектор
на малый вектор 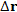 в близко расположенную точку
в близко расположенную точку 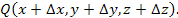
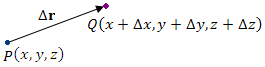
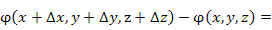
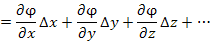 ,
,
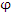 можно представить в виде
можно представить в виде
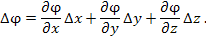
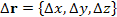 , а другим – вектор
, а другим – вектор 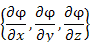 , называемый градиентом скалярного поля:
, называемый градиентом скалярного поля:
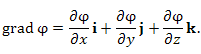
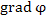 и
и 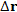 .
.
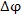 принимает наибольшее значение, если направление вектора смещения
принимает наибольшее значение, если направление вектора смещения 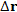 совпадает с направлением
совпадает с направлением 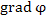 . Другими словами, вектор grad φ направлен в сторону наиболее быстрого возрастания функции φ, а его величина
. Другими словами, вектор grad φ направлен в сторону наиболее быстрого возрастания функции φ, а его величина 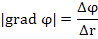 равна быстроте изменения функции
равна быстроте изменения функции 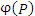 в этом направлении.
в этом направлении.
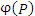 задано в плоской области. Тогда уравнение
задано в плоской области. Тогда уравнение 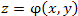 описывает некоторую поверхность в трехмерном пространстве.
описывает некоторую поверхность в трехмерном пространстве.

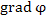 в некоторой точке показано стрелкой.
в некоторой точке показано стрелкой.
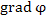 , а величина градиента определяется тангенсом угла наклона, соответствующего этому направлению.
, а величина градиента определяется тангенсом угла наклона, соответствующего этому направлению.