Потенциал точечного заряда описывается формулой 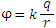 , где k – числовой множитель; q – величина заряда; r – расстояние от заряда до точки наблюдения. , где k – числовой множитель; q – величина заряда; r – расстояние от заряда до точки наблюдения.
 Напомним, что скалярное поле, величина которого зависит только от расстояния r до центра поля, называется центральным или сферическим полем. Поверхности уровня такого поля (эквипотенциальные поверхности) представляют собой концентрические сферы с центром в точке расположения источника поля.
Напомним, что скалярное поле, величина которого зависит только от расстояния r до центра поля, называется центральным или сферическим полем. Поверхности уровня такого поля (эквипотенциальные поверхности) представляют собой концентрические сферы с центром в точке расположения источника поля.
 Рис. 1
Рис. 1. Эквипотенциальные поверхности положительного точечного заряда.
Более светлые участки соответствуют областям с большими значенями поля.
(Для просмотра эквипотенциальных поверхностей отрицательного точечного заряда подведите курсор к рисунку.)
Потенциал нескольких зарядов равен сумме потенциалов, созданных каждым из зарядов по отдельности.
Если, например, заряд q1 расположен в точке 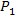 с координатами с координатами 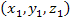 , а заряд q2 – в точке , а заряд q2 – в точке 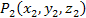 , то уравнение эквипотенциальных поверхностей имеет вид
где , то уравнение эквипотенциальных поверхностей имеет вид
где 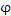 – значение потенциала. – значение потенциала.



|

|
|
| |
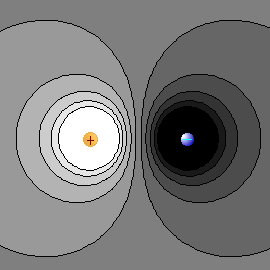
Рис. 2. Эквипотенциальные поверхности в окрестности двух зарядов с различными значениями зарядов.
Более светлые участки соответствуют областям с большими значенями поля.
|
|