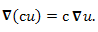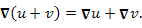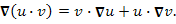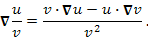Существуют различные способы задания функций, которые представляет собой те или иные правила сопоставления каждому значению одной величины соответствующее значение другой величины. Например, функция может быть задана графически, параметрически, в явном или неявном виде и т.д.
 Один из весьма плодотворных подходов, позволяющих сформулировать соотношения между функциями, основан на использовании понятия оператора, то есть последовательного набора команд, осуществляющих преобразование одной функции в другую.
Один из весьма плодотворных подходов, позволяющих сформулировать соотношения между функциями, основан на использовании понятия оператора, то есть последовательного набора команд, осуществляющих преобразование одной функции в другую.
 Например, равенство
Например, равенство 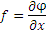 можно рассматривать в качестве правила преобразования функции можно рассматривать в качестве правила преобразования функции 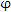 в функцию f с помощью оператора дифференцирования в функцию f с помощью оператора дифференцирования 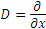 : :
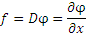 .
Подобным образом можно интерпретировать формугу для градиента скалярного поля 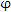 . Напомним, что . Напомним, что
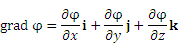 ,
где i, j и k – единичные векторы прямоугольной системы координат.
 Если формально вынести "общий множитель"
Если формально вынести "общий множитель" 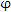 и определить оператор и определить оператор  выражением выражением
| |
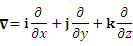 , ,
|
(1) |
|
то 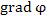 можно рассматривать как результат действия линейного дифференциального оператора можно рассматривать как результат действия линейного дифференциального оператора  на скалярную функцию на скалярную функцию 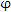 : :
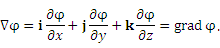 .
Таким образом,
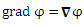 .
Приведем еще один аргумент в пользу операторной записи. Равенство 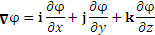 справедливо для любой скалярной функции справедливо для любой скалярной функции 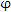 . Поэтому его можно сформулировать в символическом виде (1), убрав упоминание о . Поэтому его можно сформулировать в символическом виде (1), убрав упоминание о 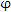 . .
 Во многих случаях с оператором
Во многих случаях с оператором  можно обращаться как с обычным вектором, роль координат которого играют операторы можно обращаться как с обычным вектором, роль координат которого играют операторы
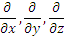 , преобразующие справа расположенную функцию в соответствующие частные производные от этой функции. , преобразующие справа расположенную функцию в соответствующие частные производные от этой функции.
 Следует, однако, иметь в виду, что операторная алгебра несколько отличается от векторной. Так, оператор
Следует, однако, иметь в виду, что операторная алгебра несколько отличается от векторной. Так, оператор  действует только на функцию, расположенную справа от оператора. Например, действует только на функцию, расположенную справа от оператора. Например, 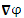 представляет собой векторную функцию, тогда как представляет собой векторную функцию, тогда как 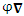 – векторный оператор, которому еще предстоит подействовать на ту функцию, которая окажется справа от него:
Свойства – векторный оператор, которому еще предстоит подействовать на ту функцию, которая окажется справа от него:
Свойства оператора оператора  . .
-
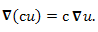
-
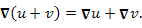
-
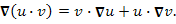
-
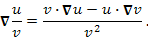
Для примера докажем справедливость свойства 3:
|
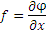 можно рассматривать в качестве правила преобразования функции
можно рассматривать в качестве правила преобразования функции 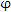 в функцию f с помощью оператора дифференцирования
в функцию f с помощью оператора дифференцирования 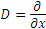 :
:
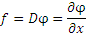 .
.
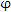 . Напомним, что
. Напомним, что
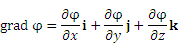 ,
,
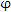 и определить оператор
и определить оператор  выражением
выражением
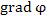 можно рассматривать как результат действия линейного дифференциального оператора
можно рассматривать как результат действия линейного дифференциального оператора  на скалярную функцию
на скалярную функцию 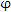 :
:
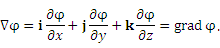 .
.
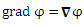 .
.
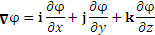 справедливо для любой скалярной функции
справедливо для любой скалярной функции 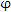 . Поэтому его можно сформулировать в символическом виде (1), убрав упоминание о
. Поэтому его можно сформулировать в символическом виде (1), убрав упоминание о 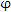 .
.
 можно обращаться как с обычным вектором, роль координат которого играют операторы
можно обращаться как с обычным вектором, роль координат которого играют операторы
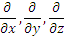 , преобразующие справа расположенную функцию в соответствующие частные производные от этой функции.
, преобразующие справа расположенную функцию в соответствующие частные производные от этой функции.
 действует только на функцию, расположенную справа от оператора. Например,
действует только на функцию, расположенную справа от оператора. Например, 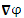 представляет собой векторную функцию, тогда как
представляет собой векторную функцию, тогда как 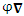 – векторный оператор, которому еще предстоит подействовать на ту функцию, которая окажется справа от него:
– векторный оператор, которому еще предстоит подействовать на ту функцию, которая окажется справа от него:
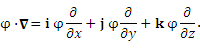
 .
.
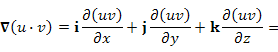
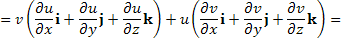
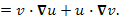
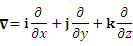 ,
,