Пусть функция 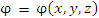 описывает некоторое скалярное поле. Выберем произвольную точку описывает некоторое скалярное поле. Выберем произвольную точку 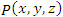 и сместимся из нее на малый вектор и сместимся из нее на малый вектор 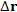 в близко расположенную точку в близко расположенную точку 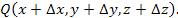 При этом значение функции При этом значение функции  изменяется на величину изменяется на величину 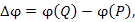
 При обсуждении градиента скалярного
поля
При обсуждении градиента скалярного
поля
Градиент скалярного поля
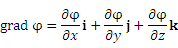 .
Вектор 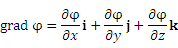 указывает направление наиболее быстрого изменения функции φ, а его величина 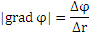 равна быстроте изменения функции φ в этом направлении.
|
было показано, что разность 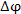 можно представить в виде скалярного произведения градиента можно представить в виде скалярного произведения градиента  и вектора смещения и вектора смещения 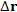 :
Разделим обе части этого равенства на величину вектора смещения. (Заметим, что отношение вектора смещения к его величине представляет собой единичный вектор :
Разделим обе части этого равенства на величину вектора смещения. (Заметим, что отношение вектора смещения к его величине представляет собой единичный вектор 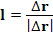 в направлении в направлении 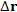 .) Далее выполним предельный переход .) Далее выполним предельный переход 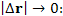
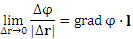 .
 Предел в левой части вышеприведенного равенства называется производной скалярного поля по направлению вектора l и записывается в виде
Предел в левой части вышеприведенного равенства называется производной скалярного поля по направлению вектора l и записывается в виде
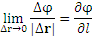 .
Таким образом, производная функции по заданному направлению равна скалярному произведению градиента функции на единичный вектор этого направления:
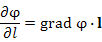 .
Поскольку вектор 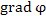 направлен с сторону наиболее быстрого возрастания функции направлен с сторону наиболее быстрого возрастания функции  , а его величина равна скорости изменения , а его величина равна скорости изменения  в этом направлении, то проекция градиента поля в этом направлении, то проекция градиента поля  на произвольное направление равна быстроте изменения функции на произвольное направление равна быстроте изменения функции  в таком направлении. в таком направлении.
 Следовательно, производная функции
Следовательно, производная функции  по направлению вектора l представляет собой скорость изменения по направлению вектора l представляет собой скорость изменения  в этом направлении. в этом направлении.
 Заметим, что понятие производной функции по направлению вектора является обобщением понятия частной производной функции. Например, частную производную
Заметим, что понятие производной функции по направлению вектора является обобщением понятия частной производной функции. Например, частную производную 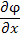 можно интерпретировать как производную функции можно интерпретировать как производную функции  по направлению вектора i, т.е. вдоль положительного направления оси 0x. по направлению вектора i, т.е. вдоль положительного направления оси 0x.
 Используя
свойство скалярного произведения векторов,
Используя
свойство скалярного произведения векторов,
|
Свойство скалярного произведения
Пусть a = {ax , ay , az}
и b = {bx , by , bz}.
Тогда ab = ax bx +
ay by + az bz.
|
формулу для производной скалярного поля по направлению вектора можно представить в координатной форме записи:
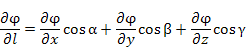 .
Здесь 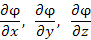 – координаты вектора – координаты вектора 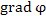 ; α, β и γ – углы, образованные вектором l с положительными направлениями координатных осей; направляющие косинусы cos α, cos β и cos γ являются координатами единичного вектора l . ; α, β и γ – углы, образованные вектором l с положительными направлениями координатных осей; направляющие косинусы cos α, cos β и cos γ являются координатами единичного вектора l .
|
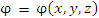 описывает некоторое скалярное поле. Выберем произвольную точку
описывает некоторое скалярное поле. Выберем произвольную точку 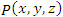 и сместимся из нее на малый вектор
и сместимся из нее на малый вектор 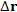 в близко расположенную точку
в близко расположенную точку 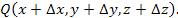 При этом значение функции
При этом значение функции  изменяется на величину
изменяется на величину 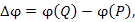
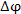 можно представить в виде скалярного произведения градиента
можно представить в виде скалярного произведения градиента  и вектора смещения
и вектора смещения 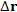 :
:
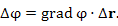
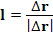 в направлении
в направлении 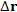 .) Далее выполним предельный переход
.) Далее выполним предельный переход 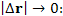
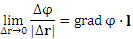 .
.
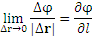 .
.
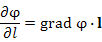 .
.
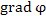 направлен с сторону наиболее быстрого возрастания функции
направлен с сторону наиболее быстрого возрастания функции  , а его величина равна скорости изменения
, а его величина равна скорости изменения  в этом направлении, то проекция градиента поля
в этом направлении, то проекция градиента поля  на произвольное направление равна быстроте изменения функции
на произвольное направление равна быстроте изменения функции  в таком направлении.
в таком направлении.
 по направлению вектора l представляет собой скорость изменения
по направлению вектора l представляет собой скорость изменения  в этом направлении.
в этом направлении.
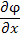 можно интерпретировать как производную функции
можно интерпретировать как производную функции  по направлению вектора i, т.е. вдоль положительного направления оси 0x.
по направлению вектора i, т.е. вдоль положительного направления оси 0x.
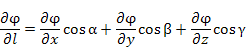 .
.
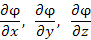 – координаты вектора
– координаты вектора 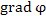 ; α, β и γ – углы, образованные вектором l с положительными направлениями координатных осей; направляющие косинусы cos α, cos β и cos γ являются координатами единичного вектора l .
; α, β и γ – углы, образованные вектором l с положительными направлениями координатных осей; направляющие косинусы cos α, cos β и cos γ являются координатами единичного вектора l .
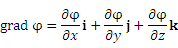 .
.
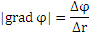 равна быстроте изменения функции φ в этом направлении.
равна быстроте изменения функции φ в этом направлении.