Закон всемирного тяготения устанавливает, что все материальные объекты притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Сила F, с которой частица с массой m притягивается к частице, имеющей массу M и находящейся на расстоянии r, описывается уравнением
Здесь r – вектор, направленный в сторону частицы с массой m. Вектор  представляет собой единичный вектор в направлении r, а коэффициент G называется гравитационной постоянной. Знак минус означает, что сила F является силой притяжения и действует в направлении, противоположном направлению вектора r. представляет собой единичный вектор в направлении r, а коэффициент G называется гравитационной постоянной. Знак минус означает, что сила F является силой притяжения и действует в направлении, противоположном направлению вектора r.
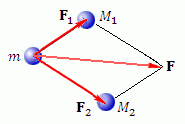
 Если имеется несколько центров притяжения, то каждый из них притягивает к себе частицу m с силой, определяемой законом всемирного тяготения, а результирующая сила равна векторной сумме сил притяжения.
Если имеется несколько центров притяжения, то каждый из них притягивает к себе частицу m с силой, определяемой законом всемирного тяготения, а результирующая сила равна векторной сумме сил притяжения.
 ,
 Энергия потенциального взаимодействия двух тел массами m и M, находящимися на расстоянии r друг от друга, описывается уравнением
Энергия потенциального взаимодействия двух тел массами m и M, находящимися на расстоянии r друг от друга, описывается уравнением
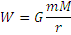 .
 Тело с массой M может рассматриваться как источник векторного поля E гравитационных сил притяжения, действующих на любые другие тела, обладающие массой. Это поле существует в каждой точке пространства и определяется равенством
Тело с массой M может рассматриваться как источник векторного поля E гравитационных сил притяжения, действующих на любые другие тела, обладающие массой. Это поле существует в каждой точке пространства и определяется равенством
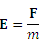 .
Иначе говоря, гравитационное поле E определяет силу, действующую со стороны поля на частицу единичной массы, то есть представляет собой векторное поле, являющееся силовой характеристикой распределения источников притяжения.
 Аналогично, потенциал гравитационного поля определяется как потенциальная энергия частицы единичной массы,
Аналогично, потенциал гравитационного поля определяется как потенциальная энергия частицы единичной массы,
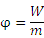 ,
и представляет собой скалярное гравитационное поле.
|
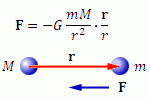
 представляет собой единичный вектор в направлении r, а коэффициент G называется гравитационной постоянной. Знак минус означает, что сила F является силой притяжения и действует в направлении, противоположном направлению вектора r.
представляет собой единичный вектор в направлении r, а коэффициент G называется гравитационной постоянной. Знак минус означает, что сила F является силой притяжения и действует в направлении, противоположном направлению вектора r.
 ,
, 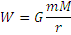 .
.
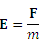 .
.
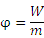 ,
,