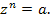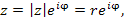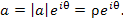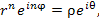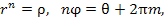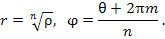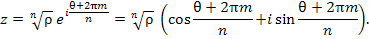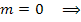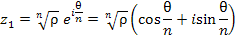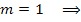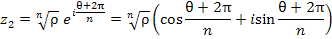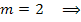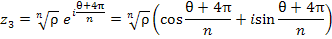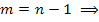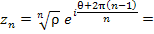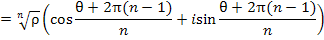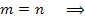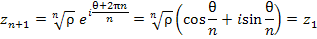| |
Число z называется корнем n-й степени из числа a, если
| |
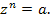
|
(1) |
|
Представим числа a и z в показательной форме:
| |
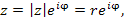
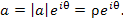
|
(2) |
|
Тогда
| |
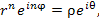
|
(3) |
|
что влечет
| |
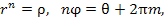
|
(4) |
|
где m – любое целое число.
 Запись аргумента nφ в виде θ + 2πm отражает тот факт, что функция
Запись аргумента nφ в виде θ + 2πm отражает тот факт, что функция 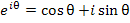 является периодической с периодом 2π. При выполнении операций сложения, умножения или деления комплексных чисел слагаемое 2πm можно опускать. Однако ситуация изменяется, когда производится возведение в степень с дробным показателем, поскольку величина 2πm/n уже не является кратной периоду 2π для произвольных целых значений m. является периодической с периодом 2π. При выполнении операций сложения, умножения или деления комплексных чисел слагаемое 2πm можно опускать. Однако ситуация изменяется, когда производится возведение в степень с дробным показателем, поскольку величина 2πm/n уже не является кратной периоду 2π для произвольных целых значений m.
 Выразим полярные координаты числа z:
Выразим полярные координаты числа z:
| |
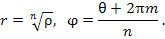
|
(5) |
|
Тогда
| |
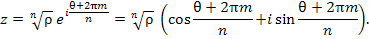
|
(6) |
|
Придавая числу m целые значения 0, 1, 2, ..., получим
Заметим, что 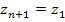 ; следующее значение m дает корень ; следующее значение m дает корень 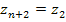 и так далее. Следовательно, существует ровно n различных корней n-ой степени из комплексного числа a. Поскольку модули корней равны между собой, то все эти корни располагаются на окружности радиуса и так далее. Следовательно, существует ровно n различных корней n-ой степени из комплексного числа a. Поскольку модули корней равны между собой, то все эти корни располагаются на окружности радиуса 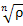 комплексной плоскости. комплексной плоскости.
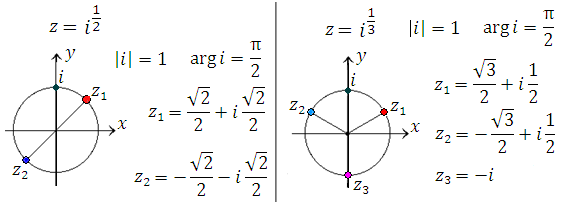
` Рис. 9. Квадратный и кубический корни из комплексного числа i.
Если известен хотя бы один из n корней комплексного числа, то остальные корни легко построить графически. Для этого нужно разделить окружность радиуса 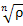 на n равных частей, начиная от точки окружности, соответствующей известному корню. Полученные точки деления представляют собой графические образы остальных корней. на n равных частей, начиная от точки окружности, соответствующей известному корню. Полученные точки деления представляют собой графические образы остальных корней.
|
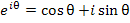 является периодической с периодом 2π. При выполнении операций сложения, умножения или деления комплексных чисел слагаемое 2πm можно опускать. Однако ситуация изменяется, когда производится возведение в степень с дробным показателем, поскольку величина 2πm/n уже не является кратной периоду 2π для произвольных целых значений m.
является периодической с периодом 2π. При выполнении операций сложения, умножения или деления комплексных чисел слагаемое 2πm можно опускать. Однако ситуация изменяется, когда производится возведение в степень с дробным показателем, поскольку величина 2πm/n уже не является кратной периоду 2π для произвольных целых значений m.
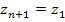 ; следующее значение m дает корень
; следующее значение m дает корень 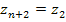 и так далее. Следовательно, существует ровно n различных корней n-ой степени из комплексного числа a. Поскольку модули корней равны между собой, то все эти корни располагаются на окружности радиуса
и так далее. Следовательно, существует ровно n различных корней n-ой степени из комплексного числа a. Поскольку модули корней равны между собой, то все эти корни располагаются на окружности радиуса 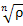 комплексной плоскости.
комплексной плоскости.
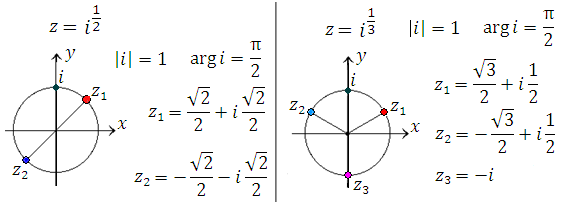
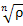 на n равных частей, начиная от точки окружности, соответствующей известному корню. Полученные точки деления представляют собой графические образы остальных корней.
на n равных частей, начиная от точки окружности, соответствующей известному корню. Полученные точки деления представляют собой графические образы остальных корней.