Для нахождения сумм вида
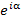 . Сумма членов такой прогрессии равна . Сумма членов такой прогрессии равна
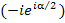 . Тогда знаменатель этой дроби становится вещественным и принимает вид . Тогда знаменатель этой дроби становится вещественным и принимает вид
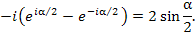 . .
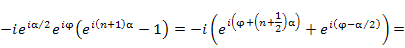
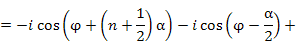
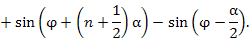
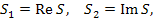
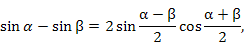
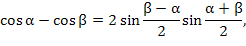
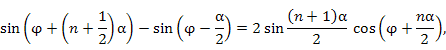
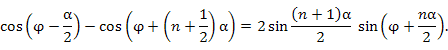
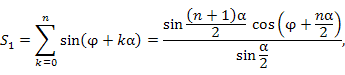
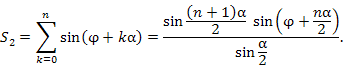
|
|
|
Для нахождения сумм вида
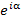 . Сумма членов такой прогрессии равна . Сумма членов такой прогрессии равна
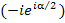 . Тогда знаменатель этой дроби становится вещественным и принимает вид . Тогда знаменатель этой дроби становится вещественным и принимает вид
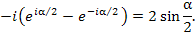 . .
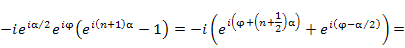
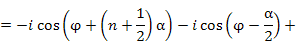
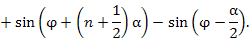
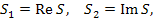
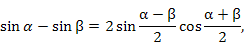
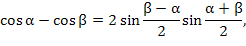
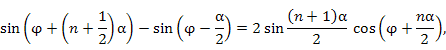
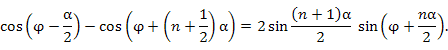
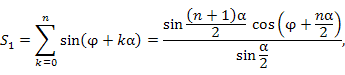
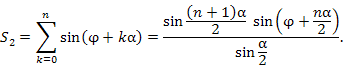
|
|
|