Конев В.В.   Комплексные числа

| Словарь | Калькулятор |
 
| Разделы курса | Примеры | Интерактивные страницы |
Основные понятия
                              Тригонометрическая форма комплексных чисел
        Рассмотрим комплексное число , изображаемое точкой на комплексной плоскости, и выразим декартовы координаты точки P через ее полярные координаты (r,φ). Тогда комплексное число принимает вид
который называется тригонометрической формой комплексного числа.
     Полярная координата r совпадает с абсолютной величиной комплексного числа z и называется также модулем z:
      Полярная координата φ называется аргументом комплексного числа z:
Аргумент φ определяется из системы уравнений
Эта система имеет бесконечное множество решений, которые отличаются друг от друга на величину 2πk, кратную периоду синуса и косинуса. Поэтому представляет собой многозначную функцию. В тех случаях, когда наличие слагаемого 2πk не является существенным, его обычно опускают, а соответствующее значение называют главным значением. Для нахождения главного значения аргумента комплексного числа z можно применять следующее простое правило:
      Иногда бывает проще нанести точку z на комплексную плоскость, чтобы найти модуль и аргумент числа из соответствующего треугольника.

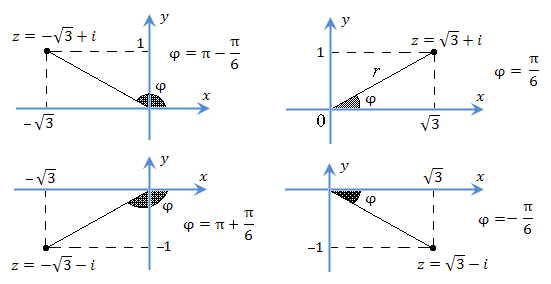
Рис. 6. Комплексные числа и их полярные координаты.
     Если комплексные числа и представлены в тригонометрической форме, то тогда и только тогда, когда
где  k - целое число.