| |
Формула Эйлера устанавливает взаимосвязь между экспоненциальной функцией 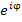 и тригонометрическими функциями и тригонометрическими функциями  и и  на множестве комплексных чисел: на множестве комплексных чисел:
| |
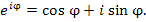 . .
|
(1) |
|
Доказательство формулы Эйлера основано на представлении этих функций в виде степенных рядов и при первом чтении может быть опущено без ущерба для понимания последующего изложения.
 Заметим, что
Заметим, что  и и  представляют собой соответственно вещественную и мнимую части экспоненциальной функции представляют собой соответственно вещественную и мнимую части экспоненциальной функции 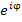 : :
| |
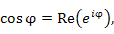 . .

|
(2) |
|
Выполним в формуле Эйлера замену  : :
| |

|
(3) |
|
Выполнив почленное сложение и вычитание выражений в обеих частях равенств (1) и (3), получим
что влечет
| |
 . .

|
(4) |
|
Таким образом, тригонометрические функции  и и  представлены в виде линейных комбинаций экспоненциальных функций представлены в виде линейных комбинаций экспоненциальных функций 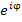 и и  . .
 Тангенс аргумента φ выражается через
Тангенс аргумента φ выражается через  : :
|
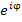 и тригонометрическими функциями
и тригонометрическими функциями  и
и  на множестве комплексных чисел:
на множестве комплексных чисел:
 и
и  представляют собой соответственно вещественную и мнимую части экспоненциальной функции
представляют собой соответственно вещественную и мнимую части экспоненциальной функции 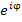 :
:
 :
:


 и
и  представлены в виде линейных комбинаций экспоненциальных функций
представлены в виде линейных комбинаций экспоненциальных функций 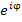 и
и  .
.
 :
:

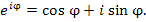 .
.
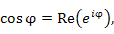 .
.


 .
.
