| |
Из теории вещественных чисел известно, что между точками числовой оси и множеством вещественных чисел x существует взаимно-однозначное соответствие: каждой точке числовой оси соответствует единственное вещественное число x, и обратно – каждому вещественному числу x соответствует единственная точка числовой оси.
 Рис. 1
Рис. 1. Числовая ось.
 Для описания положения произвольной точки P плоскости x0y необходимо задать два вещественных числа, например, декартовы координаты (x, y) точки. Каждую такую пару чисел можно рассматривать как число нового типа, называемое комплексным числом, совокупность которых образует множество комплексных чисел.
Для описания положения произвольной точки P плоскости x0y необходимо задать два вещественных числа, например, декартовы координаты (x, y) точки. Каждую такую пару чисел можно рассматривать как число нового типа, называемое комплексным числом, совокупность которых образует множество комплексных чисел.
 Комплексные числа записываются в виде
где x и y – вещественные числа; i называется мнимой единицей и определяется как число, квадрат которого равен –1:
Таким образом, комплексное число
Комплексные числа записываются в виде
где x и y – вещественные числа; i называется мнимой единицей и определяется как число, квадрат которого равен –1:
Таким образом, комплексное число 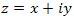 представляет собой упорядоченную пару (x, y) вещественных чисел, которые можно рассматривать как координаты точки в плоскости x0y. В таком контексте плоскость x0y называют комплексной плоскостью, а числа x и y – соответственно вещественной частью и мнимой частью комплексного числа z:
Множество комплексных чисел включает в себя в качестве подмножества совокупность вещественных чисел. Любое вещественное число x можно интерпретировать как комплексное число, мнимая часть которого равна нулю:
Числа вида z = iy, вещественные части которых равны нулю, называются чисто мнимыми. представляет собой упорядоченную пару (x, y) вещественных чисел, которые можно рассматривать как координаты точки в плоскости x0y. В таком контексте плоскость x0y называют комплексной плоскостью, а числа x и y – соответственно вещественной частью и мнимой частью комплексного числа z:
Множество комплексных чисел включает в себя в качестве подмножества совокупность вещественных чисел. Любое вещественное число x можно интерпретировать как комплексное число, мнимая часть которого равна нулю:
Числа вида z = iy, вещественные части которых равны нулю, называются чисто мнимыми.
 Между множеством комплексных чисел и множеством точек комплексной плоскости существует взаимно-однозначное соответствие, а именно: каждому комплексному числу
Между множеством комплексных чисел и множеством точек комплексной плоскости существует взаимно-однозначное соответствие, а именно: каждому комплексному числу 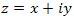 соответствует единственная точка P плоскости x0y и обратно – каждой точке P(x,y) комплексной плоскости соответствует единственное комплексное число соответствует единственная точка P плоскости x0y и обратно – каждой точке P(x,y) комплексной плоскости соответствует единственное комплексное число 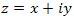 . Вещественным числа соответствуют точки оси 0x, тогда как чисто мнимым числам соответствуют точки на оси 0y. Поэтому ось 0x называют вещественной осью, тогда как ось 0y – мнимой осью. . Вещественным числа соответствуют точки оси 0x, тогда как чисто мнимым числам соответствуют точки на оси 0y. Поэтому ось 0x называют вещественной осью, тогда как ось 0y – мнимой осью.
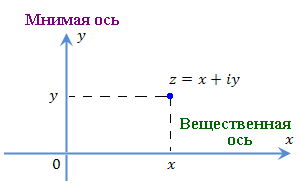 Рис. 2
Рис. 2. Комплексная плоскость.
Для изображения комплексного числа  z можно также использовать вектор с началом в точке 0 и концом в точке z. z можно также использовать вектор с началом в точке 0 и концом в точке z.
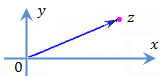 Рис. 3
Рис. 3. Векторное представление комплексного числа z.
 Абсолютная величина комплексного числа
Абсолютная величина комплексного числа 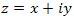 обозначается символом |z| и определяется формулой
Другое название абсолютной величины комплексного числа – модуль комплексного числа. С геометрической точки зрения абсолютная величина |z| равна расстоянию от точки z комплексной плоскости до нулевой точки. обозначается символом |z| и определяется формулой
Другое название абсолютной величины комплексного числа – модуль комплексного числа. С геометрической точки зрения абсолютная величина |z| равна расстоянию от точки z комплексной плоскости до нулевой точки.
 Число
Число 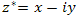 называется комплексно сопряженным числу называется комплексно сопряженным числу 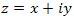 . .
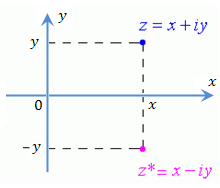 Рис. 4
Рис. 4. Комплексно сопряженные числа z и  .
|

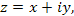
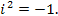
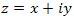 представляет собой упорядоченную пару (x, y) вещественных чисел, которые можно рассматривать как координаты точки в плоскости x0y. В таком контексте плоскость x0y называют комплексной плоскостью, а числа x и y – соответственно вещественной частью и мнимой частью комплексного числа z:
представляет собой упорядоченную пару (x, y) вещественных чисел, которые можно рассматривать как координаты точки в плоскости x0y. В таком контексте плоскость x0y называют комплексной плоскостью, а числа x и y – соответственно вещественной частью и мнимой частью комплексного числа z:

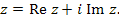
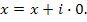
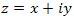 соответствует единственная точка P плоскости x0y и обратно – каждой точке P(x,y) комплексной плоскости соответствует единственное комплексное число
соответствует единственная точка P плоскости x0y и обратно – каждой точке P(x,y) комплексной плоскости соответствует единственное комплексное число 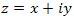 . Вещественным числа соответствуют точки оси 0x, тогда как чисто мнимым числам соответствуют точки на оси 0y. Поэтому ось 0x называют вещественной осью, тогда как ось 0y – мнимой осью.
. Вещественным числа соответствуют точки оси 0x, тогда как чисто мнимым числам соответствуют точки на оси 0y. Поэтому ось 0x называют вещественной осью, тогда как ось 0y – мнимой осью.


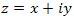 обозначается символом |z| и определяется формулой
обозначается символом |z| и определяется формулой
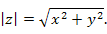
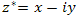 называется комплексно сопряженным числу
называется комплексно сопряженным числу 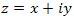 .
.

 .
.