Обратимся к рисунку 7, на котором в комплексной плоскости изображены векторы  и и  , соответствующие комплексным числам , соответствующие комплексным числам  и и  . .

Рис. 7. Векторное представление комплексных чисел.  и и 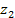
 . .
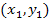 и и  справедлива формула справедлива формула
 и и  . .
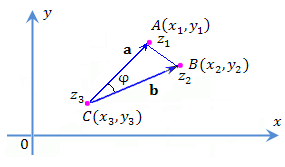
Рис. 8. Плоский треугольник, построенный на векторах a и b.
|
|
|






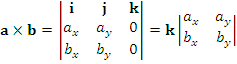 .
.



