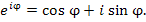Формула Эйлера
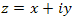 в показательной форме: в показательной форме:
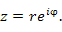
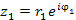 на комплексное число на комплексное число 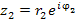 сводится к повороту вектора, соответствующего числу сводится к повороту вектора, соответствующего числу 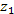 , на угол , на угол 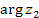 и изменению его длины в и изменению его длины в 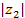 раз: раз:
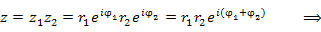
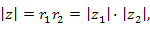
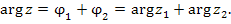
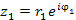 на комплексное число на комплексное число 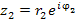 : :
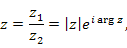
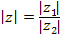 и и 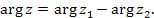
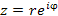 в степень n и записать результат в тригонометрической форме: в степень n и записать результат в тригонометрической форме:
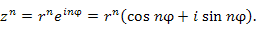
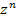 в левой части этого равенства представить в тригонометрической форме и сократить общий множитель в левой части этого равенства представить в тригонометрической форме и сократить общий множитель 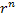 , то получится формула Муавра: , то получится формула Муавра:
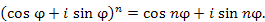 . .
|
|
|