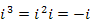|
Многие математические и физические величины описываются с помощью упорядоченных наборов чисел – примерами могут служить векторы или матрицы. К числу такого рода понятий относятся и комплексные числа, которые определяются как упорядоченные пары (x, y) вещественных чисел x и y.
Для комплексных чисел определены правила действий над ними. Суть этих правил иллюстрируется следующими двумя примерами.
В конечном итоге выясняется, что любое комплексное число (x, y) может быть представлено в виде
(x, y) = x + iy.
При этом с точки зрения алгебраических преобразований комплексных чисел все выглядит так, будто множество вещественных чисел формально дополнено мнимой единицей - с сохранением всех правил действий над вещественными числами. Следует только помнить, что каждый раз, когда встретится число i 2, его нужно заменять на (–1).
Например,
Чтобы преодолеть подобный барьер, давайте сопоставим число i с числом 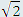 , которое тоже не очень-то просто сравнить с чем-нибудь материальным – типа количества кубиков. При этом число , которое тоже не очень-то просто сравнить с чем-нибудь материальным – типа количества кубиков. При этом число 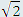 позволяет записать корни уравнения x 2 = 2 , а квадрат этого числа равен вполне понятному числу 2. позволяет записать корни уравнения x 2 = 2 , а квадрат этого числа равен вполне понятному числу 2.
В этом смысле число i столь же "нормальное", что и 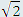 - мнимая единица позволяет записать корни уравнения x 2 = –1 , а ее квадрат выглядит и совсем просто: i 2 = –1. - мнимая единица позволяет записать корни уравнения x 2 = –1 , а ее квадрат выглядит и совсем просто: i 2 = –1.
|
|
Многие математические и физические величины описываются с помощью упорядоченных наборов чисел. Простейшими примерами могут служить векторы или матрицы. К числу такого рода понятий относятся и комплексные числа, которые определяются как упорядоченные пары (x, y) вещественных чисел x и y, удовлетворяющие заданным правилам действий над ними.
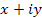 , а правила алгебраических преобразований выражений такого рода совпадают с обычными правилами действий над вещественными числами. Все выглядит так, как будто множество вещественных чисел дополнено числом нового типа, называемого мнимой единицей i, которую можно воспринимать как некий символ, но каждый раз, когда возникает число , а правила алгебраических преобразований выражений такого рода совпадают с обычными правилами действий над вещественными числами. Все выглядит так, как будто множество вещественных чисел дополнено числом нового типа, называемого мнимой единицей i, которую можно воспринимать как некий символ, но каждый раз, когда возникает число  , его следует заменять на (–1). , его следует заменять на (–1).
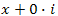 представляют собой обычные вещественные числа. Например, комплексное число представляют собой обычные вещественные числа. Например, комплексное число  есть вещественное число 5. есть вещественное число 5.
Примеры  не имеет решений (в классе вещественных чисел). Подобного рода проблема, относящаяся к уравнению не имеет решений (в классе вещественных чисел). Подобного рода проблема, относящаяся к уравнению  в свое время дала толчок к развитию множества иррациональных чисел. Поэтому введение числа i, квадрат которого равен (–1), явилось логическим шагом на пути обобщения множества вещественных чисел. в свое время дала толчок к развитию множества иррациональных чисел. Поэтому введение числа i, квадрат которого равен (–1), явилось логическим шагом на пути обобщения множества вещественных чисел.
|
|
|