Основные понятия
Полярная система координат
Полярная система координат
Для описания положения точки P плоскости x0y можно использовать полярные координаты r и φ, где r – расстояние от точки P до начала координат, называемого полюсом; φ – угол, образованный лучом 0P с положительным направлением оси 0x (полярной осью).
Полярные координаты  точки связаны с ее декартовыми прямоугольными координатами  простыми соотношениями:
 и лучи  .
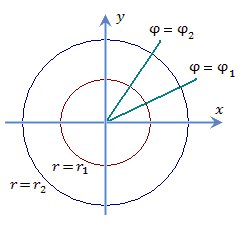
Рис. 5. Координатные линии в полярной системе координат.
|
и y = 1 – прямоугольные координаты точки P, расположенной в плоскости x0y. Тогда ее полярные координаты равны r = 2 и 
. Это означает, что точка P расположена на луче, образующем угол 
с положительным направлением оси 0x, на расстоянии двух единиц от начала координат.
– полярные координаты точки. Тогда ее декартовы координаты равны 
и 
.
 |