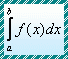| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Integrals Involving Rational Exponents |
| Key Topics Remaining: Extended List of Common Integrals |
Integrals with rational exponents 
can be transformed to integrals
of rational functions by making use the substitution x = un.
Then 
and dx = nun-1du.
Integrals with a few rational exponents can be evaluated by the substitution x = un, where n is the least common multiple of the denominators of the exponents.
Integrals involving expressions of the form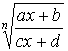 
can be evaluated by the substitution
, which eliminates the radical sign
and yields x as a rational function of u:
.
  |
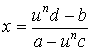