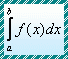| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Properties of Integrals: Comments |
| Key Topics Remaining: Table of Common Integrals » Techniques of Integration » Integration of Rational Functions » Integrals Involving Rational Exponents » Extended List of Common Integrals |
Properties 1–4 follow from the definition of indefinite integrals. Each of them can be proved by differentiation.
For example, to prove Property 4, we have to show that the expressions in both sides of the equality are primitives of the same function. Really,
![]() and
and
![]() .
.
Property 5 is based on the invariance of the form of the first differential, according to which the differential
![]()
holds its form for any composite function F (u (x)),
![]() .
.
|
|