| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Integration by Substitution: Some Important Integrals |
| Key Topics Remaining: Integration of Rational Functions » Integrals Involving Rational Exponents » Extended List of Common Integrals |
|
Problem 1. Evaluate Solution. By substitution x = at, |
| Problem 2. Evaluate Solution. By substitution x = at, |
|
Problem 3. Prove the following formula: Proof. The formula can be verified
by differentiation. We have only to check whether the derivative
of the function That is true and hence the formula. |
|
|
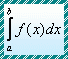
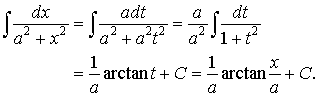
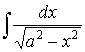
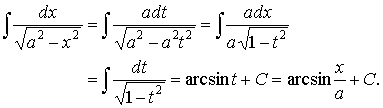
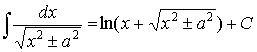 .
.