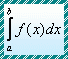| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Integration of Rational Functions: Main Definitions |
| Key Topics Remaining: Integrals Involving Rational Exponents » Extended List of Common Integrals |
A rational function f (x) can be represented by the ratio of two polynomials,
 .
.
A rational function is said to be a proper fraction, if the degree of the polynomial P (x) is less than the degree of the polynomial Q (x).
For example, the expressions
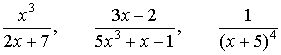 .
.
are the rational functions, the last two of which are the proper fractions, while the expression
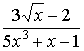
is not a rational function.
Fractions of the form
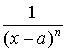 and
and 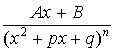
(with integer 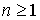 ) are called the partial
fractions, where the quadratic polynomial x2
+ px + q is assumed to be irreducible.
) are called the partial
fractions, where the quadratic polynomial x2
+ px + q is assumed to be irreducible.
A proper fraction can be decomposed into a sum of partial fractions. The corresponding method is called “Decomposition of a Rational Function into the Sum of Partial Fractions” or in short, “Partial Fraction Decomposition”.
If f (x) is not a proper fraction then it is necessary to perform the polynomial long division in order to represent f (x) by the sum of a polynomial and a proper fraction.
The integration of a polynomial is a trivial problem. Therefore, the integration of a rational function is reduced to the integration of proper fractions.
|
|