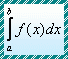| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Integration by Parts |
| Key Topics Remaining: Integration of Rational Functions » Integrals Involving Rational Exponents » Extended List of Common Integrals |
The formula of integration by parts states that
![]() (*)
(*)
for any differentiable functions u (x) and v (x).
This formula allows to transform one problem of integration to another.
If one of the two integrals, ![]() or
or ![]() , is simple, it can be used to find
the other one. This is the main idea of the method of integration by parts.
, is simple, it can be used to find
the other one. This is the main idea of the method of integration by parts.
Formula (*) can be derived in the following way:
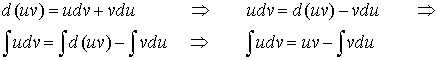
In practice, the procedure of integrating by parts consists of a few steps.
First, it is necessary to introduce intermediary functions u (x) and v (x) such that
![]() .
.
For example, one can set u (x) =f (x), which implies v'(x) = 1.
Next, one needs to differentiate u (x) and integrate v'(x) to get the differential
![]()
and the function
![]() ,
,
respectively.
Note that a constant of integration can be taken zero at this step (C = 0).
Then try to evaluate the integral ![]() .
.
The main problem one faces when dealing with the method of integration by parts is the choice of the intermediary functions. There is no general rule to follow it. It is a matter of experience and nothing more. In order to understand better this technique, it is necessary to make any choice and perform the calculations. If the obtained integral is simpler than the given one, then all is O.K. Otherwise, go back and make another choice. In such a way one can easily appreciate whether the choice of u (x) is the best.
However, you can apply the following criteria to make the right choice.
- The integral of v' should be easy for evaluation.
- The derivative of u (x) should be a simple function than u (x).
|
|