| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Partial Fractions Decomposition |
| Key Topics Remaining: » Integrals Involving Rational Exponents » Extended List of Common Integrals |
In simple cases, the decomposition of proper fractions into the sum of partial fractions can be obtained by means of elementary algebraic manipulations.
Examples:
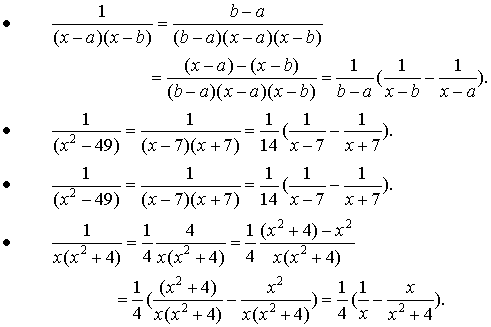
In more complicated cases, one has to use the technique of Partial Fraction Decomposition.
By the Partial Fraction Decomposition, a compound fraction is transformed into a sum of partial fractions. Therefore, this procedure is the inverse operation with respect to the reduction of a sum of fractions to a common denominator.
There exist some rules of a decomposition of any proper fraction into a sum of partial fractions.
|
|