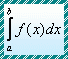| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Transformation of the Table of Derivatives to the Table of Integrals |
| Key Topics Remaining: Techniques of Integration » Integration of Rational Functions » Integrals Involving Rational Exponents » Extended List of Common Integrals |
Let us recall the derivatives of elementary functions. For instance, the power rule states that
![]() .
.
This formula can be transformed as follows.
First, substitute (n + 1) for k :
![]() .
.
Then divide both sides of the equality by (n + 1) (provided that n ≠ –1) and read the formula from right to left:
![]() .
.
Therefore, the function ![]() is a primitive of xn
, so the power rule for integration has the following form:
is a primitive of xn
, so the power rule for integration has the following form:
![]() ,
, ![]() .
.
The derivatives of all elementary functions can be treated similarly to transform the table of derivatives to the table of integrals.
|
|