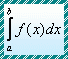| Basic Conceptions |
Primitives and Indefinite Integrals
Properties of Integrals
| Properties: Explanatory Comments |
Transformation of a Table of Common Derivatives to a Table of Integrals
A Table of Common Integrals
| Integration |
Techniques of Integration
| Integration by Substitution | ||
| ||
|
Integration by Parts |
| Integration of Rational Functions |
Basic Conceptions
Integration of Partial Fractions
Partial Fraction Decomposition
| Integration of Irrational Expressions |
Integrals Involving Rational Exponents
Integrals Involving Radicals
| Summary |
Extended List of Common Integrals
| Integration by Substitution |
| Key Topics Remaining: Integration of Rational Functions » Integrals Involving Rational Exponents » Extended List of Common Integrals |
The technique of substitutions helps to reduce many integrals to common indefinite integrals, which are given in the Table of Common Integrals.
For convenience sake all substitutions may be subdivided into two classes,
u = g (x) and x = u (t).
In both cases, we change the variable of integration – in one way or another.
As a rule, the substitution u = g (x) is used when a given integral has the following structure:
![]() .
.
Then the substitution u = g (x)
implies ![]() , so that the given problem is transformed
into another problem:
, so that the given problem is transformed
into another problem:
![]() .
.
We expect that the obtained integral is easier evaluated. Otherwise, another substitution or integration method may be required.
The technique of substitution is quite general and can be used in a wide variety of problems.
In particular, one can generalize the table of common integrals applying the technique of substitutions. Consider, for instance, the power rule:
![]() (
( ![]() ).
).
Let u (t) be any differentiable function. If we use the substitution x = u, then the power rule can be formulated as follows:
![]() .
.
This formula is exactly the same as the original power rule. The only difference is the interpretation of the symbol u as a function of a variable t and so du = u'dt. Therefore, we obtain the following generalized power rule:
![]() (
( ![]() ).
).
One can interpret each of the common integrals in a similar way by considering the variable of integration as a function.
|
|