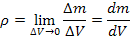Понятие поля имеет важное значение для описания процессов, изучаемых в таких областях физики как электродинамика, гидромеханика или механика сплошных сред. Различают скалярные и векторные поля.
 Если каждой точке P некоторой области D пространства поставлено в соответствие значение скалярной функции
Если каждой точке P некоторой области D пространства поставлено в соответствие значение скалярной функции 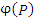 , то говорят, что в области D задано скалярное поле , то говорят, что в области D задано скалярное поле 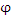 . .
 Другими словами, под скалярным полем
Другими словами, под скалярным полем 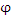 понимается скалярное функция понимается скалярное функция 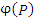 положения точки, заданная в некоторой области пространства. В прямоугольной системе координат положение точки описывается ее декартовыми координатами x, y, z и, следовательно, задание скалярного поля положения точки, заданная в некоторой области пространства. В прямоугольной системе координат положение точки описывается ее декартовыми координатами x, y, z и, следовательно, задание скалярного поля 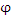 равносильно заданию скалярной функции равносильно заданию скалярной функции 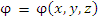 трех переменных. В частности, функция трех переменных. В частности, функция 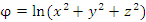 определяет скалярное поле в пространстве с выколотым началом координат. определяет скалярное поле в пространстве с выколотым началом координат.
 Простейшим примером скалярного поля является температурное поле неоднородно нагретого тела, поскольку каждой точке тела можно поставить в соответствие определенное значение температуры.
Простейшим примером скалярного поля является температурное поле неоднородно нагретого тела, поскольку каждой точке тела можно поставить в соответствие определенное значение температуры.
 Задание векторного поля в области D означает, что в этой области определена векторная функция
положения точки
Задание векторного поля в области D означает, что в этой области определена векторная функция
положения точки 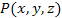 в пространстве. в пространстве.
 Например, уравнение
описывает векторное электрическое поле точечного заряда q в точке P, где k – постоянный множитель; r – вектор, проведенный из точки расположения заряда в точку P. Если заряд расположен в начале координат, то r представляет собой радиус-вектор точки P;
Например, уравнение
описывает векторное электрическое поле точечного заряда q в точке P, где k – постоянный множитель; r – вектор, проведенный из точки расположения заряда в точку P. Если заряд расположен в начале координат, то r представляет собой радиус-вектор точки P; 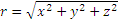 – расстояние от заряда до точки наблюдения; – расстояние от заряда до точки наблюдения;  – единичный вектор в направлении радиус-вектора. – единичный вектор в направлении радиус-вектора.
 Поля, не зависящие от времени, называются стационарными. Например, смещение точки колеблющейся струны из положения равновесия зависит не только от положения этой точки, но и от времени. Поэтому такое смещение представляет собой одномерное нестационарное скалярное поле.
Поля, не зависящие от времени, называются стационарными. Например, смещение точки колеблющейся струны из положения равновесия зависит не только от положения этой точки, но и от времени. Поэтому такое смещение представляет собой одномерное нестационарное скалярное поле.
Другие примеры скалярных полей:
-
Плотность распределения заряда.
Плотность распределения заряда
в некоторой области пространства является скалярной функцией положения точки и представляет собой предел отношения заряда ∆ q, находящегося в объеме ∆ V, к величине этого объема при стягивании ∆ V в точку:

|
-
Плотность распределения массы.
Плотность распределения массы m
в некоторой области пространства является скалярной функцией положения точки и представляет собой предел отношения массы ∆ m, находящейся в объеме ∆ V, к величине этого объема при стягивании ∆ V в точку:
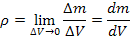
|
- Потенциал системы заряженных частиц
- Гравитационный потенциал системы тел.
- Давление в жидкой или газообразной среде, в которой распространяется звуковая волна, зависит от положения точки в пространстве и является скалярным полем.
Другие примеры векторных полей:
- Сила, действующая на единичный положительный заряд со стороны других зарядов. (Напряженность электрического поля.)
- Сила, действующая на движущийся заряд со стороны других движущихся зарядов. (Индукция магнитного поля.)
- Сила гравитационного притяжения.
- Скорость потока движущейся жидкости.
|
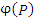 , то говорят, что в области D задано скалярное поле
, то говорят, что в области D задано скалярное поле 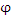 .
.
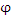 понимается скалярное функция
понимается скалярное функция 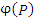 положения точки, заданная в некоторой области пространства. В прямоугольной системе координат положение точки описывается ее декартовыми координатами x, y, z и, следовательно, задание скалярного поля
положения точки, заданная в некоторой области пространства. В прямоугольной системе координат положение точки описывается ее декартовыми координатами x, y, z и, следовательно, задание скалярного поля 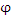 равносильно заданию скалярной функции
равносильно заданию скалярной функции 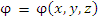 трех переменных. В частности, функция
трех переменных. В частности, функция 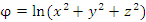 определяет скалярное поле в пространстве с выколотым началом координат.
определяет скалярное поле в пространстве с выколотым началом координат.
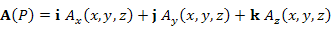
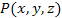 в пространстве.
в пространстве.
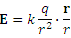
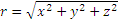 – расстояние от заряда до точки наблюдения;
– расстояние от заряда до точки наблюдения;  – единичный вектор в направлении радиус-вектора.
– единичный вектор в направлении радиус-вектора.