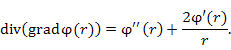Словарные статьи с заголовками на букву Д
|
Двойной интеграл
|
Интеграл от функции двух переменных по плоской области P: 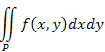 . .
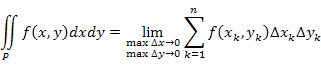 , ,
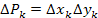 - площади элементов этой области. - площади элементов этой области.
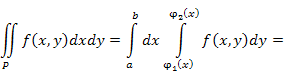
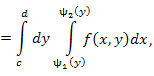
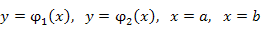
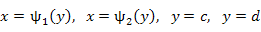
|
| Пример | Двойной интеграл от единицы по некоторой области равен площади этой области. |
|
Двойной интеграл в полярной системе координат
|
Если в двойном интеграле произвести замену переменных
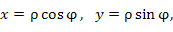
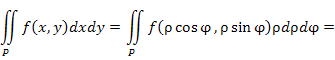
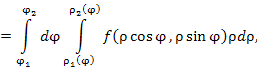
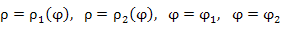
|
| Пример |
Двойной интеграл по кругу радиуса R с центром в начале координат:
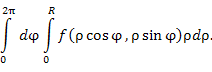
|
|
Дивергенция векторного поля
|
Скалярная функция, обозначаемая символическими выражениями 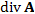 или или 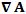 , описывающая плотность распределения источников поля: , описывающая плотность распределения источников поля:
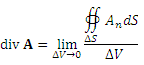 . .
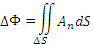 – поток векторного поля A из области, ограниченной поверхностью – поток векторного поля A из области, ограниченной поверхностью 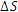 ; ; 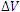 – объем этой области. – объем этой области.
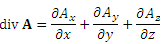 . .
|
| Интерпретация |
Одно из уравнений Максвелла устанавливает, что 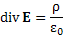 , где E – напряженность электрического поля; ρ – плотность распределения заряда. , где E – напряженность электрического поля; ρ – плотность распределения заряда.
Таким образом, функция div E описывает распределение заряда в пространстве. |
|
Дивергенция векторного поля, свойства
|
|
| Пример |
Пусть 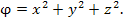 Тогда Тогда
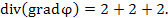
|
|
Дифференциал функции трех переменных
|
Главная линейная часть приращения функции 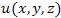 : :
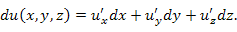
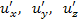 – частные производные фунции u по переменным x, y и z соответственно. Если эти частные производные представляют собой непрерывные функции, то смешанные производные не зависят от порядка дифференцирования: – частные производные фунции u по переменным x, y и z соответственно. Если эти частные производные представляют собой непрерывные функции, то смешанные производные не зависят от порядка дифференцирования:
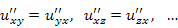
|
| Пример |
Пусть 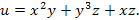 Тогда Тогда
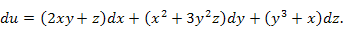
|
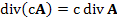
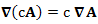 (C – константа)
(C – константа)
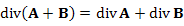
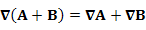
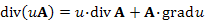
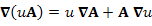
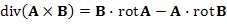
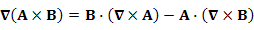
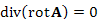
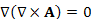
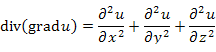
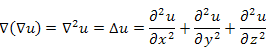
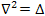 – оператор Лапласа.)
– оператор Лапласа.)