Словарные статьи с заголовками на букву С
| Скалярное поле |
Скалярнае функция 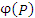 положения точки в пространстве. положения точки в пространстве.
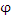 равносильно заданию скалярной функции равносильно заданию скалярной функции 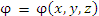 трех переменных. трех переменных.
|
| Примеры |
|
| Скалярное произведение векторов |
Число, равное произведению длин векторов на косинус угла между ними:
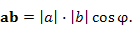
Скалярное произведение векторов a и b можно представить в виде суммы попарных произведений соответствующих координат этих векторов: 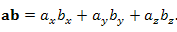
|
| Примеры | Пусть a = {3,–1, 2} и b = {5,4,3}. Тогда a · b = 17. |
| Смешанное произведение векторов |
Произведению вида 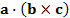
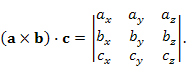
|
| Интерпретация | Смешанное произведение векторов a, b и c (с точностью до знака) равно объему параллелепипеда, построенного на этих векторах. |
| Стокса формула |
Циркуляция векторного поля A вдоль замкнутого контура L равна потоку ротора A через поверхность S, натянутую на контур L:
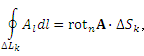
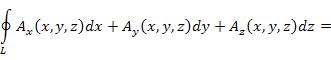
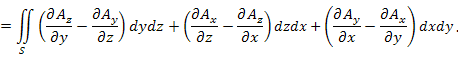
|
| Пример |
Формула Грина
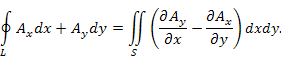
|
| Сферические координаты |
Положение точки М в сферической системе координат задается тройкой чисел r, φ и θ, где r – расстояние от начала координат до точки M (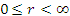 ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х ( ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (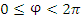 ); θ – угол между положительным направлением оси Oz и радиус-вектором точки М ( ); θ – угол между положительным направлением оси Oz и радиус-вектором точки М (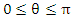 ). ).
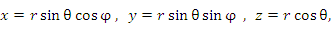
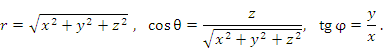
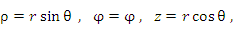
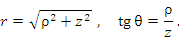
|
| Иллюстрация |
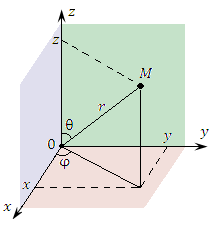
Рис. 1. Сферические координаты точки M. |