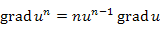Словарные статьи с заголовками на букву Г
|
Градиент скалярного поля
|
Вектор, обозначаемый символическим выражением 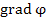 (или (или 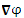 ), направленный в сторону наиболее быстрого возрастания поля ), направленный в сторону наиболее быстрого возрастания поля 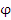 . .
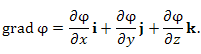
|
| Пример |
Напряженность электростатического поля E связана с потенциалом φ равенством 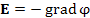 . .
Отрицательный знак перед 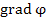 означает, что сила, действующая на положительно заряженную частицу со стороны электрического поля, направлена в сторону наиболее быстрого убывания скалярного поля. означает, что сила, действующая на положительно заряженную частицу со стороны электрического поля, направлена в сторону наиболее быстрого убывания скалярного поля. |
|
Градиент скалярного поля, свойства
|
|
| Интерпретация |
Если 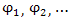 – потенциалы зарядов – потенциалы зарядов 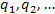 соответственно, то равенство соответственно, то равенство
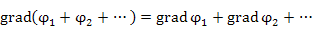
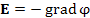 нескольких зарядов равно векторной сумме полей, образованных каждым зарядом по отдельности: нескольких зарядов равно векторной сумме полей, образованных каждым зарядом по отдельности:
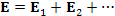
|
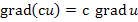
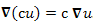
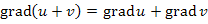
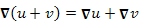
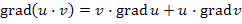
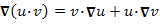
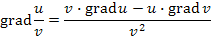
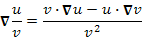
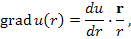 ,
,