Словарные статьи с заголовками на букву К
|
Криволинейный интеграл первого рода
|
Интеграл от скалярной функции f по дуге L : 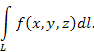
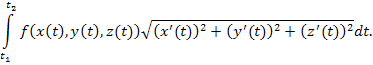
|
| Интерпретация | Пусть функция f описывает линейную плотность распределения массы вдоль линии L. Тогда интегрирование этой функции по дуге L дает массу этой линии. |
|
Криволинейный интеграл второго рода
|
Интеграл по линии L от проекции векторной функции A на направление касательной к L:
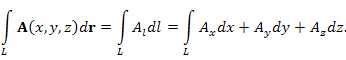
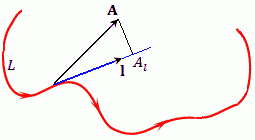
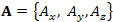 , , 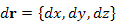 , ,
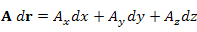 . .
|
| Интерпретация | Криволинейный интеграл от F по линии L работе силы F по перемещению частицы вдоль линии L. |
|
Коэффициенты Ламе
|
Величины
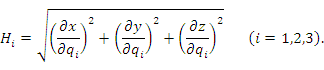
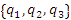 – координаты ортогональной криволинейной системы координат. – координаты ортогональной криволинейной системы координат.
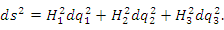
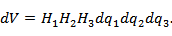
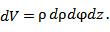
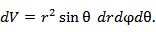
|
| Пример |
Пусть 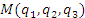 и и 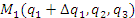 – две точки, лежащие на одной координатной – две точки, лежащие на одной координатной 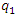 -линии. Тогда предел отношения длины дуги M M1 к приращению координаты -линии. Тогда предел отношения длины дуги M M1 к приращению координаты 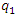 при при 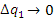 равен коэффициенту Ламе H1: равен коэффициенту Ламе H1:
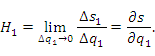
|
|
Криволинейные координаты
|
Тройка чисел q1 , q2 , q3 , поставленных в соответствие каждой точке M трехмерного пространства.
|
| Пример |
В цилиндрической системе координат
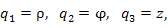
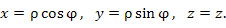
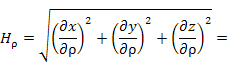
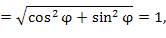
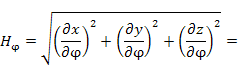
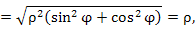
|