Словарные статьи с заголовками на букву П
| Поверхности уровня | Множество всех точек пространства с одинаковыми значениями скалярного поля. |
| Пример |
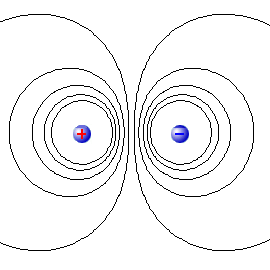
Рис. 1. Поверхности уровня в окрестности двух зарядов противоположных знаков. На рисунке показано сечение поверхностей плоскостью, проходящей через точки расположения зарядов. |
| Поверхностный интеграл первого рода |
Предел интегральной суммы вида
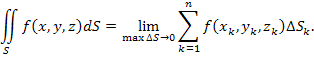
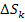 ; ; 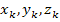 - координаты произвольной точки в k-ой ячейке. - координаты произвольной точки в k-ой ячейке.
|
| Интерпретация | Если функция f описывает плотность распределения заряда вдоль поверхности S, то интегрирование этой функции по области S дает величину заряда поверхности. |
| Поверхностный интеграл второго рода |
Интеграл по поверхности S от проекции векторной функции A на направление нормали к S :
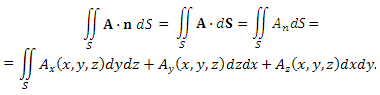
|
| Пример | Если векторную функцию A(x, y, z) интерпретировать как скорость потока течения жидкости, то интегрирование этой функции по области S дает объем жидкости, протекающей в единицу времени через поверхность S. |
| Поле векторное |
Векторная функция
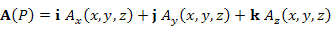
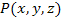 , заданная в некоторой области пространства. , заданная в некоторой области пространства.
|
| Примеры |
|
| Поле скалярное |
Скалярнае функция 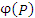 положения точки в пространстве. положения точки в пространстве.
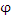 равносильно заданию скалярной функции равносильно заданию скалярной функции 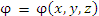 трех переменных. трех переменных.
|
| Примеры |
|
| Поле потенциальное |
Векторное поле A, которое может быть представлено в виде градиента некоторого скалярного поля φ:
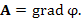
|
| Примеры |
|
| Поток векторного поля через поверхность |
Поверхностный интеграл второго рода от векторной функции A(x, y, z) по поверхности S:
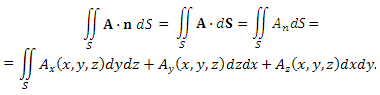
|
| Пример |
Поток векторного поля 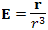 через поверхность сферы радиуса R равен 4π. через поверхность сферы радиуса R равен 4π.
|
| Производная скалярного поля по направлению вектора |
Скорость изменения скалярного поля φ в направлении, заданном вектором l:
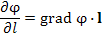
|
| Пример |
Пусть известен градиент скалярного поля φ в некоторой точке 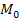 : :
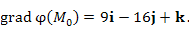
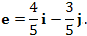 равна равна
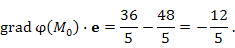
|