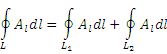Словарь математических терминов

| А | Б | В | Г | Д | Е | З | И | К | Л
| Н | О | П | Р | С | Т | Ф | Ц | Э |
Словарные статьи с заголовками на букву Ц
Центральное скалярное поле  Скалярное поле, которое зависит только от расстояния r до некоторого центра.
Поверхности уровня центрального поля представляют собой концентрические сферы с центром в точке расположения источника поля и описываются уравнением r = const.
Иллюстрация
Цилиндрическая система координат представляет собой трёхмерную систему координат, являющуюся обобщением полярной системы координат посредством добавления третьей координаты, которая задаёт смещение произвольной точки M вдоль оси 0z относительно координатной плоскости 0xy. Положение точки M в цилиндрической системе координат определяется тройкой чисел  ρ,  φ  и  z, где  ρ – расстояние от точки  M  до оси  0z (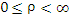);  φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси  0х (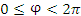);  z – проекция точки  M  на ось  0z ().
Связь между декартовыми и цилиндрическими координатами описывается формулами

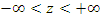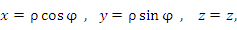
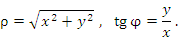
Иллюстрация

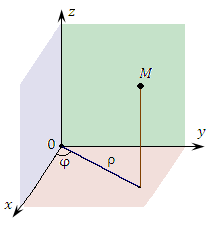
Рис. 1. Цилиндрические координаты точки M.
Цилиндрическое поле См. Аксиально-симметричное поле.
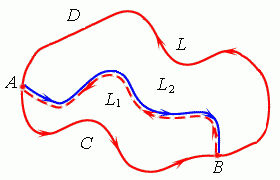
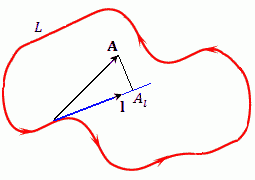
Циркуляция векторного поля Криволинейный интеграл второго рода по замкнутому контуру L:
Направление обхода контура считается положительным, если при движении по контуру ограниченная им область остается слева.
Основные свойства
  1. При изменении направления обхода контура циркуляция векторного поля изменяет свой знак на обратный:

  2. Если односвязную область, ограниченную контуром L, разбить на две части, границами которых являются контуры L1 и L2, то циркуляция векторного поля A по контуру L равна сумме циркуляций по контурам L1 и L2:

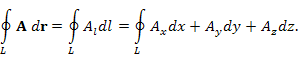
Пример Если F – сила, действующая на частицу, то циркуляция векторного поля F представляет собой работу этой силы по перемещению частицы по замкнутому контуру L.