Словарные статьи с заголовками на букву Б
|
Базис в трехмерном пространстве
|
Любая тройка некомпланарных векторов  .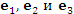
Произвольный вектор 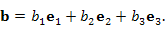 b трехмерного пространства может быть представлен, и притом единственным образом, в виде линейной комбинации базисных векторов:
|
| Пример |
Единичные попарно ортогональные векторы i, j и k образует базис в трехмерном пространстве. Тройку таких векторов обычно выбирают так, чтобы их направления совпадали с направлениями координатных осей прямоугольной системы координат, а разлзложение произвольного вектора по базисному набору векторов i, j и k записывают в виде
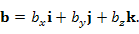
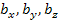 называются координатами вектора b в ортогональном базисе векторов.
|
|
Бином Ньютона
|
Формула возведения в целую степень суммы двух величин:
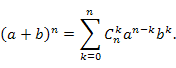
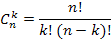 обладают следующими свойствами:
|
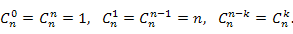
| Примеры |
|
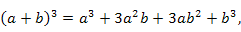
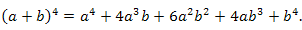