Конев В.В.   Кривые и поверхности второго порядка

Поверхности второго порядка
             Конусы
      Каноническое уравнение конуса второго порядка можно представить в виде
  (5)  
В этом случае точка O(0,0,0) является вершиной конуса, а ось 0z – осью конуса.

       
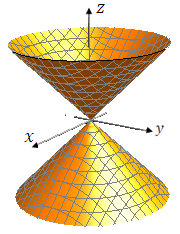
Рис. 25. Конусы второго порядка.

      Если a = b, то конус (5) называется круговым. Произвольный конус может быть получен из кругового равномерным растяжением или сжатием вдоль оси 0y. Любая плоскость, не проходящая через ось конуса, пересекает его по кривой второго порядка.
      Типичные сечения конуса плоскостями показаны на рисунках 26-29.

               
Рис. 26. Примеры плоскостей, пересекающих конус по эллипсу или окружности.

          
Рис. 27. Примеры плоскостей, пересекающих конус по гиперболе.


Рис. 28. Плоскость, проходящая параллельно образующей конуса, пересекает его по параболе.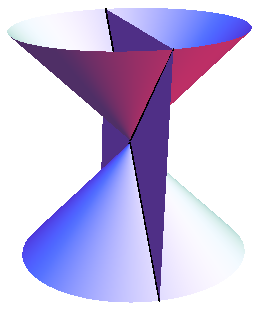

     
Рис. 29. Плоскость, проходящая ось конуса, пересекает его по паре прямых.

      Прямая, проходящая через любую точку конуса и его вершину, целиком принадлежит конусу.
      Круговой конус может быть получен вращением наклонной прямой, проходящей через его вершину, вокруг оси конуса.