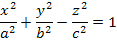Конев В.В.   Кривые и поверхности второго порядка

Поверхности второго порядка
             Гиперболоиды
      Гиперболоидом называется поверхность, которая в некоторой декартовой системе координат описывается одним из уравнений:
  (1)  
или
  (2)  
Величины a, b и c называются полуосями гиперболоида.
Уравнение (1) определяет однополостный гиперболоид, графические примеры которых представлены на рисунке 14.

          
Рис. 14. Однополостные гиперболоиды.

      Сечениями однополостных гиперболоидов плоскостями являются эллипсы (в частности, окружности) и гиперболы.

                              
Рис. 15. Сечения однополостных гиперболоидов плоскостями.

      Если a = b, то гиперболоиды, определяемые уравнением (1), является поверхностями вращения. Например, однополостный гиперболоид
образован вращением одной из ветвей гиперболы, представленной на рисунке 18, вокруг оси 0z.

Рис. 18. Гипербола с полуосями a и c, расположенная в плоскости x0z.

      Отметим, что однополостный гиперболоид вращения может быть получен вращением прямой вокруг некоторой скрещивающейся с ней прямой.