Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат описывается уравнением
Это равенство называется каноническим уравнением эллипсоида. Величины a, b и c называются полуосями эллипсоида.
Эллипсоид может быть получен равномерным сжатием или растяжением сферы вдоль трёх взаимно перпендикулярных осей. Говоря иначе, уравнение эллипсоида получается из уравнения сферы масштабным преобразованием
Если центр эллипсоида находится в точке 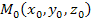 , то уравнение эллипсоида принимает вид , то уравнение эллипсоида принимает вид
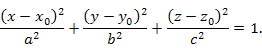
 Рис. 10
Рис. 10. Любая плоскость пересекает поверхность эллипсоида по эллипсу.
(Для изменения цвета и формы эллипсоида поместите курсор указателя мыши в область рисунка).
Эллипсоид, все оси которого различны, называется трехосным.
Если какие-либо две оси эллипсоида одинаковы, то эллипсоид называют сфероидом.
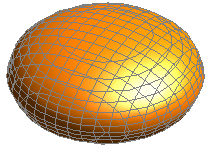 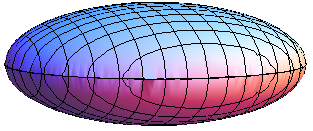 Рис. 11
Рис. 11. Сфероиды.
Сфероид представляет собой поверхность, образованную вращением половины дуги эллипса вокруг оси, соединяющей концы этой дуги. Пусть, например, b = c. Тогда эллипсоид
образован вращением верхней половины дуги эллипса, представленного на рисунке 4, вокруг оси 0x.
 Рис. 12
Рис. 12. Эллипс с полуосями a и b, расположенный в плоскости x0 y.
Если a = b = c, то эллипсоид вырождается в сферу радиуса a.
|