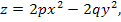Параболоидом называется поверхность, которая в некоторой декартовой системе координат описывается одним из уравнений:
Параболоид представляет собой незамкнутую нецентральную поверхность (не имеющую центра симметрии). Уравнение (3) описывает эллиптические параболоиды.    
Рис. 22. Эллиптические параболоиды. Если p = q, то параболоид (3) называется круговым и является телом вращения, образованным вращением одной ветви параболы  вокруг оси 0z. вокруг оси 0z.
Сечениями эллиптических параболоидов плоскостями являются эллипсы и параболы.  
Рис. 23. Сечения эллиптических параболоидов плоскостями. |