Сфера представляет собой геометрическое место точек пространства, равноудалённых от некоторой точки, называемой центром сферы. В декартовой системе координат сфера описывается уравнением
где 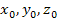 - координаты центра сферы; R – радиус сферы. - координаты центра сферы; R – радиус сферы.
Если центр сферы расположен в начале декартовой системы координат, то уравнение ее поверхности имеет вид
и называется каноническим уравнением сферы, а соответствующая система координат называется канонической.
Сфера – идеально симметричная фигура. Ее поворот вокруг любой оси, проходящей через центр, сохраняет форму фигуры и ее местоположение. Можно также сказать, что поверхность сферы образована вращением полуокружности вокруг своего диаметра.
 Рис. 9
Рис. 9. Любая плоскость пересекает поверхность сферы по окружности.
(Для изменения цвета сферы поместите курсор указателя мыши в область рисунка).
Напомним, что поверхность S называется поверхностью вращения вокруг оси Oz, если для любой точки 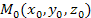 этой поверхности окружность, проходящая через эту точку в плоскости этой поверхности окружность, проходящая через эту точку в плоскости 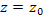 с центром в с центром в 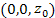 и радиусом и радиусом 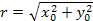 , целиком принадлежит этой поверхности. , целиком принадлежит этой поверхности.
|