Уравнение (2) определяет двухполостный гиперболоид.
 
Рис. 19. Двухполостные гиперболоиды. Сечениями двухполостных гиперболоидов плоскостями являются эллипсы и гиперболы.   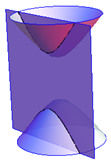  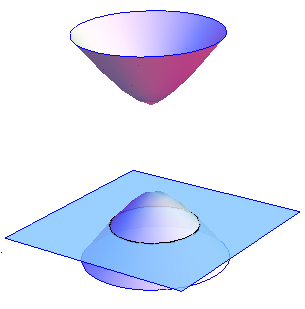 
Рис. 20. Сечения двухполостных гиперболоидов плоскостями. Если a = b, то гиперболоиды, определяемые уравнением (2), является поверхностями вращения. Например, двухполостный гиперболоид 

Рис. 21. Гипербола с полуосями a и c, расположенная в плоскости x0z. Отметим, что двухполостный гиперболоид вращения является геометрическим местом точек, модуль разности расстояний от которых до двух заданных точек, называемых фокусами гиперболоида, есть величина постоянная. |
