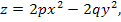Уравнение (4) описывает гиперболический параболоид:
Гиперболический параболоид представляет собой незамкнутую нецентральную поверхность (не имеющую центра симметрии).   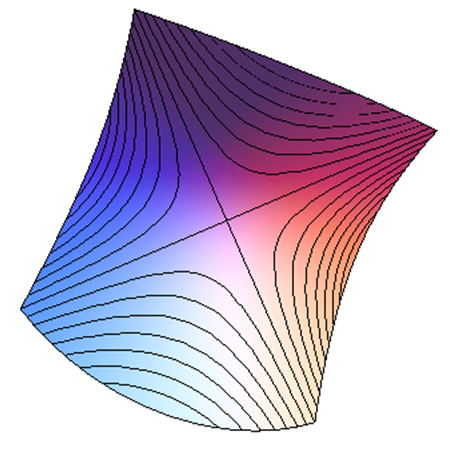
Рис. 24. Гиперболические параболоиды. Сечениями гиперболических параболоидов являются гиперболы и параболы.     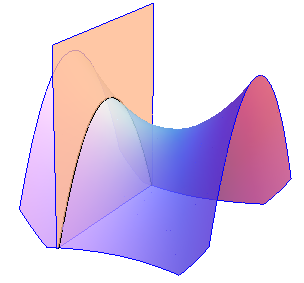 
Рис. 25. Сечения гиперболических параболоидов плоскостями. Если один из коэффициентов p или q равен нулю, то параболоид (4) называется цилиндрическим. |