Т
|
Теорема о корнях многочлена
|
Теорема. Пусть 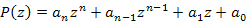 - многочлен целой степени с вещественными коэффициентами - многочлен целой степени с вещественными коэффициентами 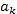 , где k = 0, 1, 2, ... Если число , где k = 0, 1, 2, ... Если число 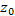 является корнем уравнения является корнем уравнения 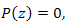 то и комплексно сопряженное число то и комплексно сопряженное число 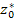 является корнем этого уравнения. является корнем этого уравнения.
Доказательство можно посмотреть в разделе "Алгебраические операции" |
|
|
|
|
Тождественное преобразование алгебраического выражения
|
заключается в замене этого выражения тождественно равным ему. Все верные числовые равенства также называются тождественными. |
|
|
|
|
Тождество
|
это равенство, справедливое при всех допустимых значениях, входящих в него переменных. |
| Пример |
Равенство 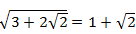
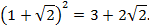
|
|
|
|
|
Тригонометрическая форма комплексного числа
|
Выражение вида
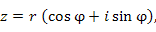
|
| Пример |
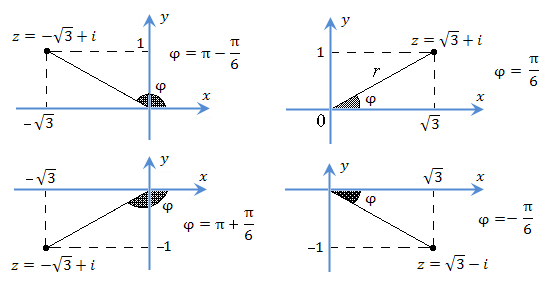
|
|
|
|
|
|
|