Н
|
Наибольший общий делитель целых чисел
|
это наибольшее натуральное число, на которое каждое из данных целых чисел делится без остатка.
Для обозначения наибольшего общего делителя двух целых чисел m и n используется символическое выражение НОД(m, n). |
| Пример |
Наибольший общий делитель чисел 12 и 30 равен 6, поскольку 6 - наибольшее натуральное число, на которое без остатка делится каждое из чисел, 12 и 30. |
|
|
|
|
Наименьшее общее кратное целых чисел
|
это наименьшее натуральное число, которое без остатка делится на каждое из данных целых чисел.
Для обозначения наибольшего общего делителя двух целых чисел m и n используется символическое выражение НОК(m, n). |
| Пример |
Наименьшее общее кратное чисел 12 и 30 равно 60, поскольку 60 - наименьшее натуральное число, которое без остатка делится на каждое из чисел, 12 и 30. |
|
|
|
|
Натуральные числа
|
возникли из потребности простого счета (перечисления): первый, второй, третий и так далее, то есть представляют собой числа вида
1, 2,3, 4, ...
Совокупность натуральных чисел образует множество, обозначаемое символом N. Принадлежность числа x к множеству натуральных чисел записывается в виде 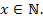
|
|
|
|
|
Неправильная дробь
|
См. словарную статью "Дробь". |
|
|
|
|
Нечетные числа
|
Целое число m называется нечетным, если число m/2 не является целым.
Если n - некоторое целое число, то число 2n + 1 является нечетным. |
|
|
|