Десятичная дробь
|
Представление десятичного числа
в виде
называется десятичной дробью, где 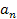 - десятичные цифры; , - десятичная запятая, отделяющая целую часть числа от дробной. Часто вместо десятичной запятой используется десятичная точка. - десятичные цифры; , - десятичная запятая, отделяющая целую часть числа от дробной. Часто вместо десятичной запятой используется десятичная точка.
 В записи целого числа отсутствуют цифры после десятичной запятой. При этом обычно опускается и сам знак десятичной запятой.
В записи целого числа отсутствуют цифры после десятичной запятой. При этом обычно опускается и сам знак десятичной запятой.
 Конечная десятичная дробь содержит конечное число цифр после запятой либо имеет нулевую дробную часть.
Конечная десятичная дробь содержит конечное число цифр после запятой либо имеет нулевую дробную часть.
 Если последовательность цифр после запятой является бесконечной, то десятичная дробь называется бесконечной.
Если последовательность цифр после запятой является бесконечной, то десятичная дробь называется бесконечной.
 Бесконечная десятичная дробь вида
называется периодической. Такая запись означает, что последовательность цифр после запятой, начиная с некоторого номера, включает в себя повторяющуюся группу цифр.
Бесконечная десятичная дробь вида
называется периодической. Такая запись означает, что последовательность цифр после запятой, начиная с некоторого номера, включает в себя повторяющуюся группу цифр.
 Можно показать, что любое действительное число может быть представлено в виде десятичной дроби.
Можно показать, что любое действительное число может быть представлено в виде десятичной дроби.
|
| Примеры
|
–5 0 3 17/2 12/28 1000

12,431 0,12 15,0 10 –4

3,(857142) = 3, 857142857142857142...= 27/7

0.(3) = 0, 333333333...= 1/3

π = 3,1415926...
|
|
Диаграммы Венна
|
используются для схематичного изображение пересечений и объединений нескольких множеств.
|
| |
|
|
Дистрибутивность
|
Свойство дистрибутивности описывается формулой

( a ± b) c = a c ± b c,
|
|
Дробь
|
Пусть рациональное число записано в виде отношения 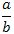 двух целых чисел a и b. Если a < b (без учета знаков), то такая дробь называется правильной; в противном случае она называется неправильной и представляет собой число, большее или равное единице (по модулю). Для приведения неправильной дроби к правильной ее числитель нужно разделить на знаменатель, выделив целую часть. Например,
Здесь 2 – целая часть неправильной дроби 14/5; 4/5 – правильная дробь. двух целых чисел a и b. Если a < b (без учета знаков), то такая дробь называется правильной; в противном случае она называется неправильной и представляет собой число, большее или равное единице (по модулю). Для приведения неправильной дроби к правильной ее числитель нужно разделить на знаменатель, выделив целую часть. Например,
Здесь 2 – целая часть неправильной дроби 14/5; 4/5 – правильная дробь.
 Часто сумму вида
Часто сумму вида 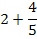 записывают как записывают как 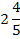 и называют смешанной дробью. Другими словами, смешанной дробью называется запись числа, содержащая целую и дробную части. Простая дробь содержит лишь числитель и знаменатель. и называют смешанной дробью. Другими словами, смешанной дробью называется запись числа, содержащая целую и дробную части. Простая дробь содержит лишь числитель и знаменатель.
|
|