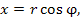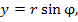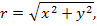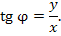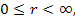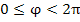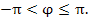П
|
Пересечение множеств
|
Пересечением множеств A и B называется множество элементов 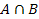 , содержащихся в A и B одновременно. , содержащихся в A и B одновременно.
|
|||||
| Примеры |
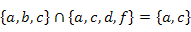
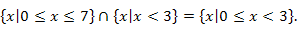
|
|||||
|
|
||||||
|
Периодическая десятичная дробь
|
См. словарную статью "Десятичная дробь". | |||||
|
|
||||||
|
Показательная форма комплексного числа
|
Выражение вида
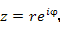
|
|||||
|
|
||||||
|
Положительные числа
|
Числа, большие нуля, называются положительными. Положительным числам соответствуют точки на числовой оси, расположенные справа от нуля.
Все положительные числа упорядочены в возрастающем порядке слева направо (с правой стороны от нуля). |
|||||
|
|
||||||
|
Полубесконечный интервал
|
См. словарную статью "Интервал". | |||||
|
|
||||||
|
Полуоткрытый интервал
|
См. словарную статью "Интервал". | |||||
|
|
||||||
|
Полярные координаты
|
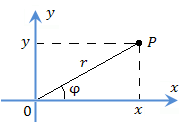
Для описания положения точки P плоскости x0y можно использовать полярные координаты r и φ, где r – расстояние от точки P до начала координат, называемого полюсом; φ – угол, образованный лучом 0P с положительным направлением оси 0x (полярной осью).
Полярные координаты 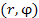 точки связаны с ее декартовыми прямоугольными координатами точки связаны с ее декартовыми прямоугольными координатами 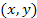 простыми соотношениями: простыми соотношениями:
|
|||||
|
|
||||||
|
Правильная дробь
|
См. словарную статью "Дробь". | |||||
|
|
||||||
|
Пропорции
|
Равные дроби называются пропорциями. Пропорции можно решать по правилу перекрестного умножения:
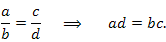
|
|||||
|
|
||||||
|
Простые дроби
|
См. словарную статью "Дробь". | |||||
|
|
||||||
|
Простые числа
|
Простым числом называется натуральное число, большее единицы, которое делится без остатка только на единицу и само на себя. Все остальные натуральные числа, кроме 1, называются составными. Последовательность простых чисел начинается с числа 2.
Все натуральные числа, большие единицы, относятся к простым или составным. Не существует формулы, позволяющей находить простые числа. Простые числа образуют бесконечное множество. |
|||||
|
|
||||||
|
Противоположное число
|
Для любого вещественного числа a существует противоположное число (–a), которое в сумме с a дает нуль:
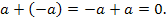
|
|||||
|
|
||||||
|
Процент
|
Термин процент используется для обозначения одной сотой части (или доли) от некоторой величины и обозначается символом %. Например, 12 % от 200 означает 0.12∙200 = 24.
Величины можно сравнивать между собой по разности их значений. Однако, это далеко не всегда позволяет получить реальное представление о соотношении между ними. Пусть, например, одна величина больше другой на 9 единиц. Если первая из этих величин равна 1, то вторая превосходит ее в 9 раз. Напротив, если одна их величин равна 1000000, а другая отличается от нее на 10 единиц, то это фактически означает их примерное равенство. От подобного недостатка свободно сравнение величин в процентах. В первой из двух вышеупомянутых ситуаций можно было бы сказать, что значение второй величины составляет 900 % от первой, тогда как во втором случае различие между величинами составляет лишь 0.001 %. (Последний результат получен делением разности на меньшее из двух чисел с последующим умножением на 100 % |
|||||
|
|
||||||
|
Пустое множество
|
Пустое множество не содержит ни одного элемента и поэтому всегда может рассматриваться как строгое подмножество любого множества. | |||||
|
|
||||||